Περί της ισχύος της Ειδικής Θεωρίας της Σχετικότητας

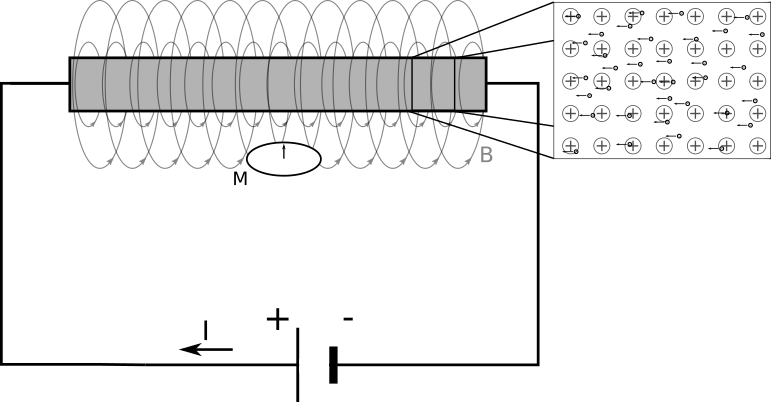
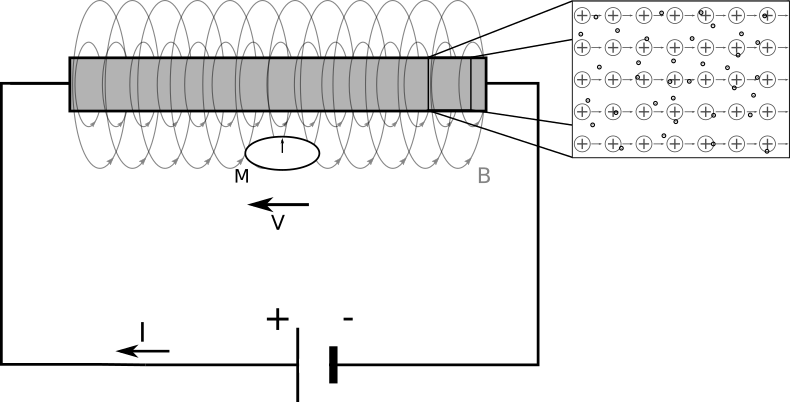
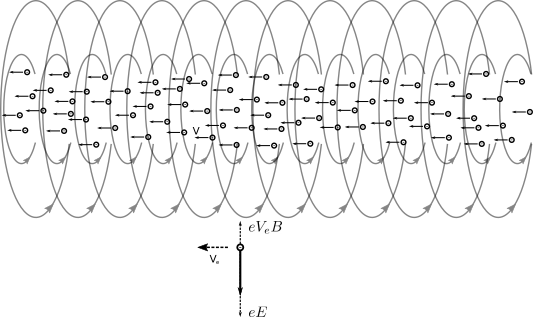
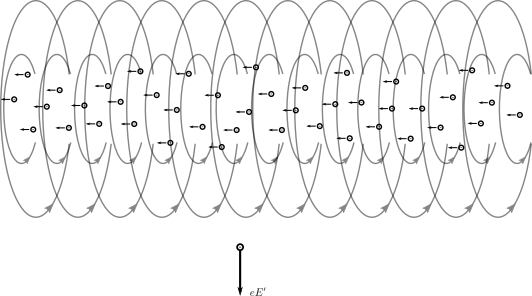
Γράφει ο Μιχάλης Παπαχρήστου

Στο τεύχος Νο.30 (Δεκέμβριος του '19) του περιοδικού Physics News της Ένωσης Ελλήνων Φυσικών (ΕΕΦ) παρουσιάστηκε ένα άρθρο το οποίο ισχυριζόταν την κατάρριψη της Ειδικής Θεωρίας της Σχετικότητας (ΕΘΣ) μέσω ενός απλού πειράματος.

Το πείραμα περιγράφεται ως εξής:
Έστω ένας αγωγός ο οποίος συνδέεται με μια πηγή συνεχούς ρεύματος μέσω ενός καλωδίου στο οποίο έχουμε και ένα διακόπτη. Κάτω από τον αγωγό έχουμε τοποθετήσει μια μαγνητική βελόνα (π.χ. μια πυξίδα). Όσο ο διακόπτης είναι ανοιχτός, δηλαδή δεν υπάρχει ροή ρεύματος στο καλώδιο και στον αγωγό, τότε δεν θα έχουμε κανένα μαγνητικό πεδίο και η πυξίδα θα μείνει ακίνητη. Στη συνέχεια, κλείνουμε το διακόπτη και κατά συνέπεια το κύκλωμα διαρρέεται από ηλεκτρικό ρεύμα, δηλαδή από τη συλλογική κίνηση των ελεύθερων ηλεκτρονίων του αγωγού. Τα τελευταία κινούνται με μια ταχύτητα V σε σχέση με το εργαστήριό μας, άρα και σε σχέση με την ακίνητη πυξίδα. Όπως γνωρίζουμε, ένα ηλεκτρικό ρεύμα δημιουργεί ένα μαγνητικό πεδίο και ειδικότερα για την περίπτωση ενός κυλινδρικού αγωγού (ή ενος καλωδίου) έχει κυκλική φορά, σαν να "αγκαλιάζει" τον αγωγό. Το μαγνητικό αυτό πεδίο αλληλεπιδρά με την πυξίδα με αποτέλεσμα αυτή να μετακινείται στη θέση όπου "δείχνει" προς το χαρτί (ή την οθόνη).

Το κύκλωμα με το διακόπτη κλειστό. Ο αγωγός διαρέεται από ηλεκτρικό ρεύμα και άρα έχουμε μαγνητικό πεδίο που μετράει η πυξίδα M. Η κίνηση των ηλεκτρονίων στη πραγματικότητα είναι αντίθετη από τη καθιερωμένη, για ιστορικούς λόγους, κατεύθυνση του ηλεκτρικού ρεύματος

Τώρα, κινούμε την πυξίδα κατά τη φορά της ροής των ηλεκτρονίων (αντίθετα από το ηλεκτρικό ρεύμα) με ταχύτητα V. Αυτό έχει σαν συνέπεια η πυξίδα να μην "βλέπει" την κίνηση των ηλεκτρονίων αφού κινείται με την ίδια ταχύτητα με αυτά και άρα δεν υπάρχει σχετική κίνηση μεταξύ τους. Η κατάσταση αυτή, κατα το συγγραφέα του άρθρου, είναι ισοδύναμη με τη κατάσταση όπου ο διακόπτης είναι ανοιχτός όποτε δεν υπάρχει μαγνητικό πεδίο και άρα η πυξίδα θα παραμένει σταθερή, δηλαδή έχουμε ένα παράδοξο.

Στην πραγματικότητα όμως, ένας αγωγός αποτελείται όχι μόνο από ελεύθερα ηλεκτρόνια, αλλά και από δέσμια θετικά φορτία (τα άτομα από τα οποία διέφυγαν τα ηλεκτρόνια και έμειναν θετικά φορτισμένα). Καθώς κινούμαστε λοιπόν μαζί με τα ηλεκτρόνια, τότε δεν αντιλαμβανόμαστε ένα ρεύμα ηλεκτρονίων αλλά ένα ρεύμα θετικών φορτίων να κινείται προς την αντίθετη κατεύθυνση με ταχύτητα μέτρου V. Εφόσον έχουμε ρεύμα έχουμε και μαγνητικό πεδίο, άρα η πυξίδα θα μας δείξει την ίδια μέτρηση. Έτσι, σε αυτό το παράδειγμα, δεν καταρρίπτεται η κλασσική φυσική και σίγουρα δεν καταρρίπτεται η σχετικότητα αφού η περίπτωση "κατάσταση του συστήματος με τον διακόπτη ανοιχτό" δεν είναι ισοδύναμη με την κατάσταστη η πυξίδα κινείται, απλά από άλλο σύστημα αναφοράς.

Το κύκλωμα με το διακόπτη κλειστό. Η πυξίδα και εμείς σαν παρατηρητές κινούμαστε με τη ταχύτητα των ηλεκτρονίων κατα μήκος του αγωγού με αποτέλεσμα τα ηλεκτρόνια στο δικό μας (και της πυξίδας) σύστημα αναφορας να είναι ακίνητα ενώ τα θετικά ιόντα να κινούνται αντίθετα.

Με αφορμή αυτό το πείραμα όμως είναι ευκαιρία να μιλήσουμε και για το πραγματικό παράδοξο της κλασσικής φυσικής. Ας απλουστεύσουμε το παραπάνω πείραμα βάζοντας στη θέση της πυξίδας ένα φορτίο (π.χ. ένα ηλεκτρόνιο). Επίσης, θα μείνουμε αρχικά στην περίπτωση της απλής δέσμης ηλεκτρονίων σαν ρεύμα, οπότε δεν υπάρχουν δέσμια θετικά φορτία. Αν το ηλεκτρόνιο είναι ακίνητο σε σχέση με το εργαστήριό μας, δίπλα από τη δέσμη η οποία κινείται, τότε θα δεχθεί μια απωστική δύναμη Coulomb από αυτήν, αφού αρνητικό φορτίο έχει η δέσμη, αρνητικό και το ηλεκτρόνιο. Παρότι η δέσμη δημιουργεί μαγνητικό πεδίο, το ακίνητο ηλεκτρόνιο δεν επηρεάζεται καθώς η δύναμη σε ένα φορτίο λόγω ενός μαγνητικού πεδίου εξαρτάται από το μαγνητικό πεδίο και την ταχύτητα του φορτίου, ενώ η διεύθυνσή της είναι κάθετη και στα δύο.

Όπως και πριν, αν τοποθετήσουμε το σύστημα αναφοράς μας πάνω σε ένα από τα ηλεκτρόνια της δέσμης, αν κινηθούμε δηλαδή μαζί με τη δέσμη, τότε το ηλεκτρόνιο θα κινείται με ταχύτητα -V όμως τώρα δεν θα υπάρχει μαγνητικό πεδίο. Και στις δύο περιπτώσεις λοιπόν, η δύναμη που θα δεχθεί το ηλεκτρόνιο από τη δέσμη θα είναι η ίδια.

Ας θεωρήσουμε όμως τώρα, ότι και το ηλεκτρόνιο κινείται με μια ταχύτητα Ve παράλληλα και με την ίδια φορά με αυτήν της δέσμης. Σύμφωνα με τα προηγούμενα η συνολική δύναμη που θα δεχθεί το ηλεκτρόνιο αποτελείται από δύο συνιστώσες, μία απωστική δύναμη πρός τα κάτω, όπως βλέπουμε το σχήμα, Fc =e E όπου E η ένταση του ηλεκτρικού πεδίου που δημιουργεί η δέσμη, $e$ το φορτίο του ηλεκτρονίου, και μια συνιστώσα κάθετη στο μαγνητικό πεδίο, FB =eVe B όπου Ve η ταχύτητα του ηλεκτρονίου και B η ένταση του μαγνητικού πεδίου. Εφόσον το μαγνητικό πεδίο είναι πρός το χαρτί (ή την οθόνη) όπως βλέπουμε στο σχήμα, η δύναμη αυτή θα είναι ελκτική προς τη δέσμη (προς τα πάνω), αν η ταχύτητα είναι ομόρροπη με την ταχύτητα των ηλεκτρονίων της δέσμης ή απωστική αν η ταχύτητα του ηλεκτρονίου είναι αντίρροπη με την ταχύτητα των ηλεκτρονίων της δέσμης (έχοντας πάρει υπόψην μας φυσικά ότι το φορτίο του ηλεκτρονίου είναι αρνητικό).

Σχηματική απεικόνιση της δέσμης των ηλεκτρονίων και ενός ηλεκτρόνιου κινούμενου με ταχύτητα Ve. Η συνολική δύναμη Lorentz είναι η ηλεκτρική δύναμη Coulomb και η μαγνητική δύναμη. Λόγω της σχετικής κίνησης στο σύστημα αναφοράς του ηλεκτρονίου

Τώρα θα μπορούσαμε να μεταφερθούμε πάλι στο σύστημα αναφοράς της δέσμης, αλλά είναι πιο ενδιαφέρον να μεταφερθούμε στο σύστημα αναφοράς του ηλεκτρονίου. Δηλαδή κινούμαστε με ταχύτητα Ve με αποτέλεσμα το ηλεκτρόνιο τώρα να είναι σταθερό και τελικά, σύμφωνα με τον ορισμό της δύναμης Lorentz, η μαγνητική δύναμη να μηδενίζεται!

Κοιτώντας δηλαδή το σύστημα από δύο διαφορετικά συστήματα αναφοράς, έχουμε διαφορετικές δυνάμεις. Αυτό, όπως καταλαβαίνουμε, έρχεται σε σύγκρουση με τη βασική αρχή ότι οι νόμοι της φυσικής θα πρέπει να είναι ίδιοι ανεξαρτήτως θέσης, διεύθυνσης και ταχύτητας οποιουδήποτε συστήματος αναφοράς.

Εδώ είναι που συναντάμε και τα όρια της κλασσικής φυσικής, δηλάδη της Νευτώνειας μηχανικής και του Γαλιλαϊκού τρόπου μετασχηματισμού συντεταγμένων που χρησιμοποιήσαμε στα παραπάνω παραδείγματα. Οι νόμοι του ηλεκτρομαγνητισμού, ή αλλιώς οι εξίσωσεις του Maxwell, δεν παραμένουν αναλλοίωτοι απλά προσθέτοντας ή αφαιρώντας ταχύτητες και θέσεις κατά τους Γαλιλαϊκούς μετασχηματισμούς, όταν κινούμαστε από το ένα σύστημα αναφοράς στο άλλο. Το 1905 ο Δανός φυσικός Hendrik Lorentz ανακάλυψε ένα σετ μετασχηματισμών οι οποίοι διατηρούν αναλλοίωτη τη φυσική των εξισώσεων του ηλεκτρομαγνητισμού. Οι μετασχηματισμοί αυτοί, που φέρουν και το όνομά του, στη συνέχεια ερμηνεύθηκαν από τον Albert Einstein και ενσωματώθηκαν στην ειδική θεωρία της σχετικότητας.

Οι μετασχηματισμοί Lorentz προβλέπουν ότι υπάρχει μια μέγιστη ταχύτητα στο σύμπαν (δηλαδή μια ταχύτητα με την οποία συνδέονται αιτιακά δύο γεγονότα), η οποία συμβολίζεται με c και η τιμή της καθορίζεται από τις σταθερές των εξισώσεων Maxwell περίπου στα 300000 χιλιόμετρα το δευτερόλεπτο. Η ταχύτητα αυτή είναι γνωστή και σαν ταχύτητα του φωτός καθώς είναι η ταχύτητα με την οποία διαδίδεται μια διαταραχή του ηλεκτρομαγνητικού πεδίου. Οι μετασχηματισμοί Lorentz σε ταχύτητες πολύ μικρότερες από αυτήν του φωτός δεν διαφέρουν από αυτές του Γαλιλαίου με αποτέλεσμα να μπορούμε να χρησιμοποιούμε άνετα τη Νευτώνεια φυσική χωρίς να έχουμε προβλήματα. Καθώς όμως κινούμαστε με ταχύτητες συγκρίσιμες με αυτήν του φωτός εμφανίζονται φαινομένα έξω από τη καθημερινή μας νευτώνια εμπειρία, όπως η διαστολή/συστολή του χρόνου και του χώρου.

Ας θεωρήσουμε για παράδειγμα ότι βρισκόμαστε στο δρόμο και παρατηρούμε ένα λεωφορείο το οποίο κινείται με ταχύτητα κοντά στην ταχύτητα του φωτός. Τότε το μήκος του όπως το μετράμε εμείς είναι μικρότερο. Ο λόγος που συμβαίνει αυτή η συστολή του μήκους καθώς και άλλα φαινόμενα ξεφεύγουν από τα πλαίσια αυτού του άρθρου (όχι ότι δεν έχουμε ξεφύγει ήδη), αλλά μπορούμε διαισθητικά να τα ερμηνεύσουμε στη μέγιστη πεπερασμένη ταχύτητα που συνδέει τα δύο άκρα του λεωφορείου στα οποία αναφερόμαστε σαν γεγονότα (καθώς μπορούν να προσδιοριστούν με μια θέση και μια χρονική στιγμή) και τα οποία αιτιακά συνδέονται με την ταχύτητα του φωτός. Με απλά λόγια, δεν γίνεται να συμβεί ένα γεγονός στην αρχή του λεωφορείου και τα αποτελέσματά του να μεταφερθούν στο τέλος του με ταχύτητα μεγαλύτερη απο αυτή του φωτός.

Ας επιστρέψουμε, επιτέλους, στο πρόβλημα με τη δέσμη ηλεκτρονίων και το αντίστοιχα κινούμενο ηλεκτρόνιο. Είχαμε μείνει στην κατάσταση όπου βρισκόμαστε πάνω στο κινούμενο ηλεκτρόνιο με συνέπεια η δύναμη από το μαγνητικό πεδίο να είναι μηδέν. Ο μόνος τρόπος η συνολική δύναμη στο ηλεκτρόνιο να είναι ίδια και στα δύο συστήματα αναφοράς, είναι η ηλεκτρική δύναμη Coulomb να είναι διαφορετική ώστε να καλύπτει τη διαφορά της μαγνητικής δύναμης όταν αλλάζουμε σύστημα αναφοράς, δηλαδή η ηλεκτρική δύναμη να είναι ανάλογη της σχετικής κίνησης των ηλεκτρονίων της δέσμης.  

Η ηλεκτρική απωστική δύναμη εξαρτάται από την πυκνότητα των ηλεκτρονίων που απαρτίζουν τη δέσμη, δηλαδή, αν μεταφερθούμε πάνω στη δέσμη πόσα ηλεκτρόνια θα υπάρχουν ανά 1 μέτρο για παράδειγμα. Από δω και πέρα θα κάνουμε αλλαγές μεταξύ των συστημάτων αναφοράς μέσω του μετασχηματισμού Lorentz, το οποίο με λίγα λόγια σημαίνει ότι βρισκόμενοι πάνω στο ηλεκτρόνιο η δέσμη θα διασταλεί κατα τη διεύθυνση της κίνησης και τα ηλεκτρόνια θα αραιώσουν. Ο λόγος που τώρα έχουμε διαστολή μήκους και όχι συστολή οφείλεται στο ότι κινούμενοι με τη φορά τη δέσμης η ταχύτητα της δέσμης ώς προς το ηλεκτρόνιο είναι μικρότερη. Έχουμε θεωρήσει ότι η δέσμη δεν έχει αρχή και τέλος, άρα αυτό που παρατηρούμε είναι η μείωση της πυκνότητας των ηλεκτρονίων (τα ίδια ηλεκτρόνια σε μεγαλύτερο μήκος) άρα και μείωση της απωστικής δύναμης Coulomb. Αξίζει να προσέξουμε ότι το μέγεθος της ταχύτητας Ve δεν έχει μεγάλη σημασία, δηλαδή δεν είναι αναγκαστικό να συγκρίνεται με την ταχύτητα του φωτός όπως στη πλειονότητα των σχετικιστικών φαινομένων. Αυτό οφείλεται στην τεράστια ισχύ των ηλεκτρικών δυνάμεων, καθώς ακόμα και μια εξαιρετικά μικρή μειοψηφούσα ποσότητα φορτίων δημιουργεί μια μετρήσιμη, για την ανθρώπινη κλίμακα, διαφορά στη συνολική δύναμη.

Αφήνουμε στον αναγνώστη να σκεφτεί τι μπορεί να συμβεί σε διαφορετικές περιπτώσεις ταχυτήτων (μεγαλύτερη από τη ταχύτητα της δέσμης, αντίθετη κλπ) αλλά και την "ρεαλιστική" περίπτωση ενός αγωγού, δηλαδή την ύπαρξη αρνητικών και θετικών φορτίων, καθως και να αποδείξει μαθηματικά τις παραπάνω ισότητες. Για την επαλήθευση τους μπορείτε να διαβάσετε τη διάλεξη 13 των διαλέξεων του Feynman (στα αγγλικά εδώ).

Συμπεραίνουμε λοιπόν ότι, όχι μόνο δεν καταρρίπτεται η θεωρία της σχετικότητας του Einstein αλλά στη πραγματικότητα μόνο αυτή μπορεί να εξηγήσει το φαινόμενο. Αξίζει εν τέλει, να αντιληφθούμε το εντυπωσιακό γεγονός ότι ένα τόσο απλό και καθημερινό φαινόμενο εξηγείται μέσω της ειδικής θεωρίας της σχετικότητας, μια θεωρία που την έχουμε συνδέσει κυρίως με περισσοτερο εξωτικά και μεγαλύτερης κλίμακας φαινόμενα.

Σχηματική απεικόνιση της δέσμης των ηλεκτρονίων και ενός ηλεκτρόνιου κινούμενου με ταχύτητα Ve αν θεωρήσουμε οτι κινούμαστε και εμεις με την ίδια ταχύτητα. Η συνολική δύναμη τώρα αποτελείται μόνο από μια μικρότερη δύναμη Coulomb καθώς το ηλεκτρικό πεδίο δημιουργείται από μια δέσμη με λιγότερα, ανα μήκος, ηλεκτρόνια.

Ευχαριστώ θερμά τον Αναπληρωτή Καθηγητή του Τμήματος Φυσικής Αθήνας κ. Νεκτάριο Βλαχάκη για τις πολύτιμες παρατηρήσεις του κατά τη συγγραφή του άρθρου.