|
Γράφει η Αφροδίτη Νάση και η Πηνελόπη Αγγελοπούλου Στα προηγούμενα Τεύχη του Physics Time, αναφερθήκαμε στους διάφορους πληθυσμούς φορτισμένων σωματιδίων που περιέχει η γήινη μαγνητόσφαιρα (βλέπε Άρθρο 1ου Τεύχους: Παγιδευμένα φορτισμένα σωματίδια γύρω από τη Γη), και εξετάσαμε τον τρόπο με τον οποίο ένα φορτισμένο σωματίδιο καταλήγει να εκτελεί γυροκίνηση γύρω από μία μαγνητική δυναμική γραμμή (βλέπε Άρθρο 2ου Τεύχους: Γυροκίνηση – ο Lorentz και η έλικα). Σε αυτό το άρθρο θα δούμε κάποιες χαρακτηριστικές ιδιότητες αυτής της κίνησης, που θα μας υποδείξουν το πώς οδηγούμαστε στην κίνηση ανάκλασης/αναπήδησης κατά μήκος μιας μαγνητικής δυναμικής γραμμής. Σύμφωνα με τη γενικότερη περίπτωση, η οποία αναλύθηκε στο 2ο Τεύχος, σε ένα σωματίδιο μάζας m και φορτίου q, το οποίο κινείται με ταχύτητα V και επιτάχυνση a, σε περιοχή με μαγνητικό πεδίο B και ηλεκτρικό πεδίο E, στο οποίο ασκείται και μια εξωτερική δύναμη F, θα ασκείται η συνολική δύναμη: Είδαμε ότι στην πιο απλή περίπτωση των παραπάνω, όπου το σωματίδιο κινείται σε περιοχή στην οποία υπάρχει ένα ομογενές και σταθερό μαγνητικό πεδίο, απουσία ηλεκτρικού πεδίου, και απουσία εξωτερικής δύναμης, τότε η δύναμη γίνεται: F = q (V x B). Χωρίζοντας την ταχύτητα σε δυο επιμέρους συνιστώσες, Vκάθετη + V//, και ορίζοντας ως οδηγό κέντρο (guiding center) το κέντρο της κυκλικής τροχιάς, είδαμε ότι τελικά το φορτίο εκτελεί δυο επιμέρους κινήσεις:
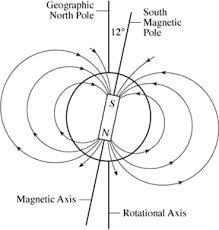
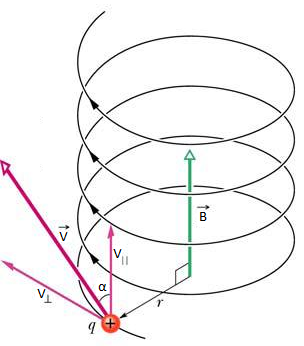
Εικόνα 1: Ο ορισμός του οδηγού κέντρου ως το κέντρο της κυκλικής κίνησης που εκτελούν τα σωματίδια γύρω από το μαγνητικό πεδίο, και ο διαχωρισμός των κινήσεων στην κίνηση του οδηγού κέντρου (κατά μήκος της μαγνητικής γραμμής), και του πραγματικού σωματιδίου (που κινείται κυκλικά γύρω από το οδηγό κέντρο). (Πηγή και Πηγή) Βρισκόμαστε, δηλαδή, στην ανάλυσή μας στο σημείο όπου ένα σωματίδιο, ή πιο σωστά, το οδηγό κέντρο της κίνησής του, κινείται με σταθερή ταχύτητα Vgc κατά μήκος μιας μαγνητικής δυναμικής γραμμής του γεωμαγνητικού πεδίου. Γνωρίζουμε όμως, ότι οι δυναμικές γραμμές εκκινούν στο Βόρειο Μαγνητικό (και αντίστοιχα Νότιο Γεωγραφικό) Πόλο και τερματίζουν στο Νότιο Μαγνητικό (και αντίστοιχα Βόρειο Γεωγραφικό) Πόλο. Επιπλέον, από τη γεωμετρία του γεωμαγνητικού πεδίου, γνωρίζουμε πως οι δυναμικές γραμμές είναι πιο αραιές στο ισημερινό επίπεδο, και πιο πυκνές προς τους πόλους. Αυτό σημαίνει ότι, πλησιάζοντας προς τους πόλους, η ένταση του γεωμαγνητικού πεδίου αυξάνεται – ή, στην περίπτωση που μελετάμε, το πεδίο παύει πια να θεωρείται σταθερό και ομογενές, όπως θεωρήσαμε παραπάνω. Τί συμβαίνει λοιπόν με την κίνηση του σωματιδίου; Εικόνα 2: Απλοποιημένη απεικόνιση του μαγνητικού πεδίου της Γης κοντά στην επιφάνειά της. Πηγή: Professor Kenneth R. Lang, Tufts University. Για να απαντήσουμε σε αυτό το ερώτημα, θα απλοποιήσουμε το συλλογισμό μας ορίζοντας κάποιες ποσότητες που θα μας βοηθήσουν στην ανάλυσή μας. Η πρώτη είναι η γωνία κλίσης (pitch angle), που συμβολίζεται με α, και ορίζεται ως η γωνία που σχηματίζει η συνολική ταχύτητα του σωματιδίου με το άνυσμα του γεωμαγνητικού πεδίου. Διαφορετικά, η εφαπτομένη της γωνίας κλίσης α ορίζεται ως ο λόγος της κάθετης προς την παράλληλη ταχύτητα: tan(a) = VL/Vgc το οποίο μας δίνει: Με τη βοήθεια της γωνίας κλίσης, οι συνιστώσες της ταχύτητας μπορούν πλέον να γραφούν ως: VL=Vsin(α) και Vgc=Vcos(α). Εικόνα 3: Η γωνία κλίσης όπως ορίζεται από τα ανύσματα της ταχύτητας και του μαγνητικού πεδίου. (Πηγή) .Η δεύτερη σημαντική ποσότητα που θα ορίσουμε, είναι η πρώτη αδιαβατική αναλλοίωτη (adiabatic invariant), που συμβολίζεται με μ και ονομάζεται μαγνητική ροπή. Οι αδιαβατικές αναλλοίωτες είναι ποσότητες οι οποίες προκύπτουν σε φυσικά συστήματα τα οποία παρουσιάζουν περιοδικές κινήσεις. Προκύπτουν από το ολοκλήρωμα της δράσης, δηλαδή από το ολοκλήρωμα της γενικευμένης ορμής του σωματιδίου κατά μήκος της τροχιάς μιας περιοδικής κίνησης. Θεωρούνται διατηρούμενες όταν το σύστημα παρουσιάζει πολύ αργές μεταβολές. Στην περίπτωση της γήινης μαγνητόσφαιρας, οι περιοδικές κινήσεις είναι οι τρεις χαρακτηριστικές κινήσεις των σωματιδίων, στις οποίες αντιστοιχεί από μια αδιαβατική αναλλοίωτη. Οι μεταβολές του συστήματος προκαλούνται από γεωμαγνητικές διαταραχές, επομένως οι αδιαβατικές αναλλοίωτες διατηρούνται όταν οι γεωμαγνητικές διαταραχές έχουν περιόδους μεγαλύτερες από τις περιόδους των τριών χαρακτηριστικών κινήσεων των σωματιδίων. Ως τώρα έχουμε δει την πρώτη από αυτές, την γυροκίνηση, και η περιοδική κίνηση που μας ενδιαφέρει για να υπολογίσουμε την πρώτη αδιαβατική αναλλοίωτη είναι η ομαλή κυκλική κίνηση που διαγράφει το σωματίδιο γύρω από το οδηγό κέντρο, δηλαδή η κίνηση Larmor. Η κίνηση αυτή, με ταχύτητα , και με τη δύναμη Lorentz να δρα ως κεντρομόλος δύναμη, δίνει κάποιες ποσότητες που θα χρησιμοποιήσουμε.
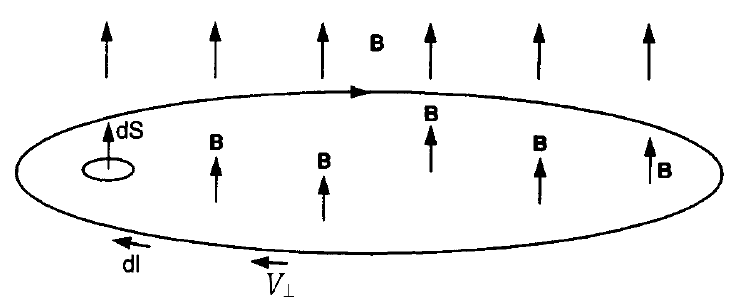
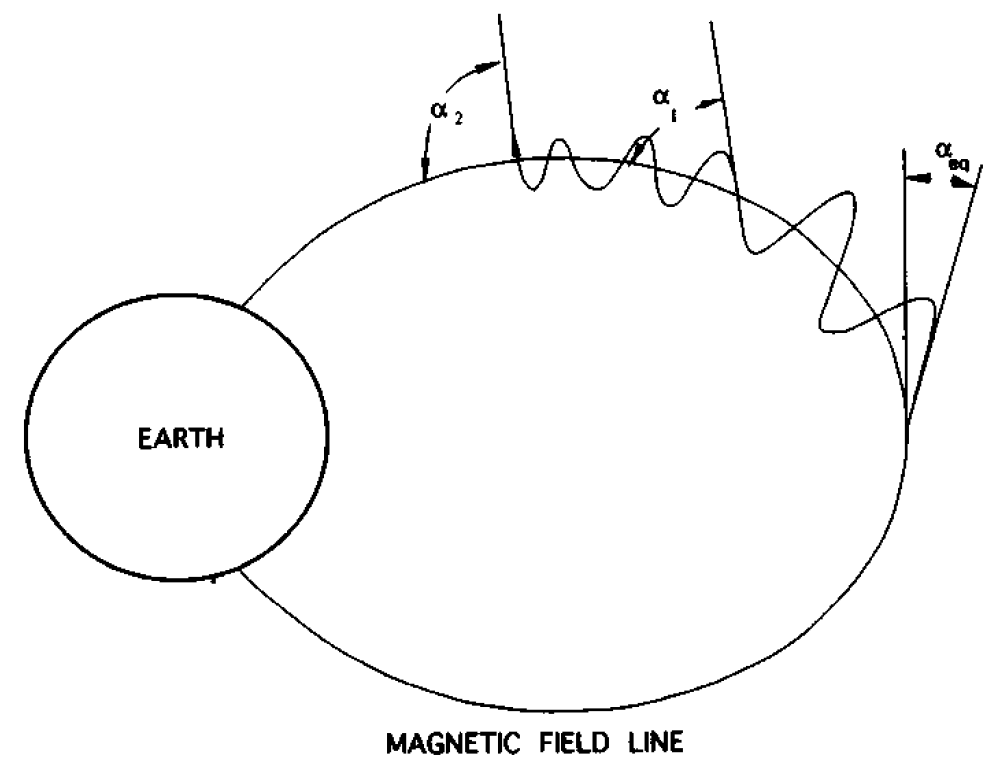
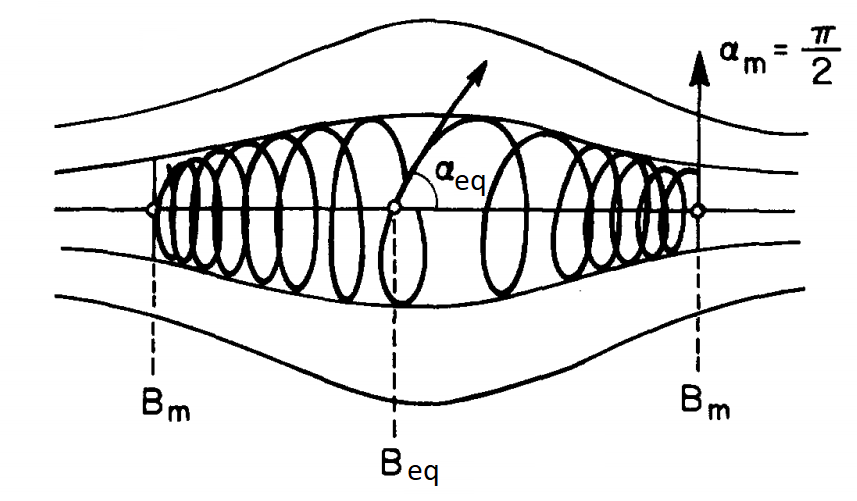
Σύμφωνα με τα παραπάνω, η 1η αδιαβατική αναλλοίωτη (μαγνητική ροπή) ισούται με το ολοκλήρωμα δράσης της γενικευμένης ορμής του σωματιδίου κάθετα στο μαγνητικό πεδίο κατά μήκος της κλειστής κυκλικής τροχιάς του σωματιδίου. Η τροχιά εκτελείται μέσα σε μαγνητικό πεδίο Β, το οποίο θεωρούμε ότι προέρχεται από ένα δυναμικό Α ως B=rotA. Η ορμή του σωματιδίου ορίζεται ως pL=mVL, αλλά η γενικευμένη ορμή του είναι: Ορίζοντας το στοιχείο μήκους κατά μήκος της τροχιάς ως dl, με φορά όμοια με της ταχύτητας VL, ολοκληρώνουμε και παίρνουμε τη δράση: Εικόνα 4: Μια προβολή της ομαλής κυκλικής κίνησης που εκτελεί ένα (θετικά φορτισμένο) σωματίδιο κάθετα στο μαγνητικό πεδίο που υπάρχει στο χώρο. Η φορά της (κάθετης) ταχύτητας καθορίζει και το στοιχείο μήκους dl του ολοκληρώματος. Το στοιχείο εμβαδού dS ορίζεται στο εσωτερικό της τροχιάς και έχει φορά όμοια με του πεδίου. Οι ορισμοί αυτοί χρησιμοποιούνται για τον υπολογισμό του ολοκληρώματος της δράσης για την κίνηση αυτή, το οποίο μας δίνει την πρώτη αδιαβατική αναλλοίωτη μ. Πηγή: Walt, Introduction to Geomagnetically Trapped Radiation. Αντί όμως για τη δράση , ως πρώτη αδιαβατική αναλλοίωτη ορίζουμε την ποσότητα μ: την οποία ονομάζουμε μαγνητική ροπή. Η αδιαβατική αυτή αναλλοίωτη θεωρούμε ότι διατηρείται όταν οι μεταβολές που παρουσιάζει το μαγνητικό πεδίο είναι αρκούντως μικρές, σε σχέση πάντα με τις χαρακτηριστικές ποσότητες της κίνησης στην οποία αναφέρονται. Δηλαδή, οι σχετικές χρονικές μεταβολές του μαγνητικού πεδίου θα πρέπει να συμβαίνουν πολύ πιο αργά από την περίοδο της κυκλικής κίνησης: και οι σχετικές χωρικές μεταβολές του μαγνητικού πεδίου θα πρέπει να είναι πολύ μικρές στην κλίμακα της γυροακτίνας: Αφού υπολογίσαμε τη γωνία κλίσης α και την 1η αδιαβατική αναλλοίωτη μ, μπορούμε επιτέλους να απαντήσουμε στο ερώτημά μας: Τί συμβαίνει κατά την κίνηση του σωματιδίου καθώς οι μαγνητικές δυναμικές γραμμές πυκνώνουν και τερματίζονται στους Πόλους; Αφού θεωρήσαμε πως οι αδιαβατικές αναλλοίωτες μένουν σταθερές υπό ορισμένες προϋποθέσεις, αυτό σημαίνει ότι: μ = σταθ. Επεξεργαζόμαστε λίγο τη σχέση για την ποσότητα μ: Θεωρώντας ότι η κινητική ενέργεια του σωματιδίου μένει σταθερή κατά τη γυροκίνηση, καταλήγουμε στο ότι και η δεύτερη ποσότητα του γινομένου θα πρέπει να παραμένει σταθερή, δηλαδή: Καθώς το σωματίδιο κινείται κατά μήκος των δυναμικών γραμμών προς την Γη, το μαγνητικό πεδίο Β αυξάνεται, δηλαδή πρέπει και το sin(α) να αυξηθεί, αφού ο λόγος τους πρέπει να παραμένει σταθερός, άρα να αυξηθεί η γωνία κλίσης α. Όταν η γωνία α αυξηθεί τόσο ώστε να γίνει 90 μοίρες, το σωματίδιο ανακλάται, επιστρέφει στον ισημερινό και επαναλαμβάνει την κίνησή του στο αντίθετο ημισφαίριο. Εικόνα 5: Η γωνία κλίσης α αυξάνεται καθώς το σωματίδιο πλησιάζει στους πόλους, όπου το μαγνητικό πεδίο είναι ισχυρότερο. Όταν γίνει ίση με 90ο το σωματίδιο ανακλάται και συνεχίζει την κίνησή του στο άλλο ημισφαίριο. Πηγή: Walt, Introduction to Geomagnetically Trapped Radiation. Επομένως, το σωματίδιο βρίσκεται παγιδευμένο μέσα σε μία “μαγνητική φιάλη”, εκτελώντας μία περιοδική κίνηση μεταξύ των δύο κατοπτρικών σημείων ανάκλασης στα δυο ημισφαίρια. Η κίνηση αυτή του οδηγού κέντρου μεταξύ των δύο σημείων ανάκλασης, ονομάζεται κίνηση ανάκλασης ή αναπήδησης (bounce motion), και είναι η δεύτερη από τις τρεις χαρακτηριστικές κινήσεις που εκτελούν τα παγιδευμένα φορτισμένα σωματίδια στη γήινη μαγνητόσφαιρα. Εικόνα 6: Η μαγνητική φιάλη που σχηματίζεται λόγω της ανάκλασης των σωματιδίων μεταξύ δυο σημείων. (Πηγή) Η εξίσωση: δίνει την γωνία σε οποιαδήποτε θέση της τροχιάς του σωματιδίου, αν το Β εκεί είναι γνωστό. Δίνει επίσης το στο σημείο ανάκλασης ως συνάρτηση των σε οποιαδήποτε άλλη θέση. Συνήθως χρησιμοποιούμε την τιμή του πεδίου και της γωνίας κλίσης στο ισημερινό (equatorial) επίπεδο, και . Γνωρίζοντας αυτές, μπορούμε να κατασκευάσουμε μια σχέση μου μας δίνει τις αντίστοιχες τιμές τους στο σημείο όπου το σωματίδιο ανακλάται (mirror) ως εξής: Όμως στο σημείο ανάκλασης είναι , και άρα: είναι η σχέση που μας δίνει την τιμή του πεδίου στο σημείο ανάκλασης. Είναι προφανές από αυτή τη σχέση, ότι για πολύ μικρές τιμές της ισημερινής γωνίας κλίσης αeq η τιμή του πεδίου στο σημείο ανάκλασης BM θα είναι πολύ μεγάλη. Σε αυτή την περίπτωση το σωματίδιο μπορεί να μην συναντήσει ποτέ το απαιτούμενο μαγνητικό πεδίο για να ανακλαστεί και θα χαθεί στην ατμόσφαιρα καθώς συνεχίζει να κινείται κατά μήκος της δυναμικής γραμμής. Αν τώρα η τιμή της αeq είναι πολύ μεγάλη, τότε η τιμή του πεδίου στο σημείο ανάκλασης θα είναι πολύ μικρή, και το σωματίδιο θα ανακλάται κοντά στο ισημερινό επίπεδο. Για =90° το σωματίδιο βρίσκεται παγιδευμένο στον Ισημερινό. Αντίστοιχα, αν γνωρίζουμε τις τιμές του πεδίου Βeq και BM, μπορούμε να βρούμε την ισημερινή γωνία κλίσης του σωματιδίου από τη σχέση: Σε επόμενο άρθρο θα δούμε πώς η κίνηση αναπήδησης ορίζει τη δεύτερη αδιαβατική αναλλοίωτη, η διατήρηση της οποίας οδηγεί στην τρίτη χαρακτηριστική κίνηση των σωματιδίων, την κίνηση ολίσθησης.
Βιβλιογραφία
Comments are closed.
|
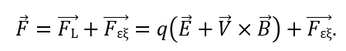

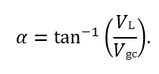
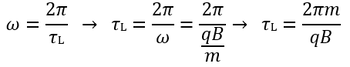
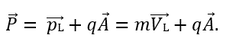
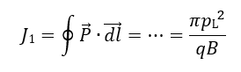
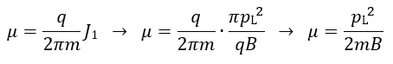
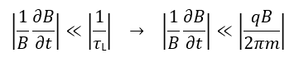
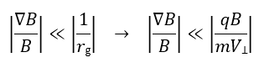
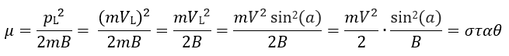
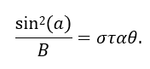
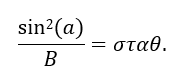
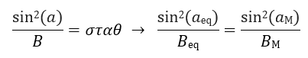
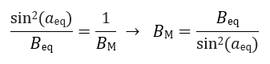
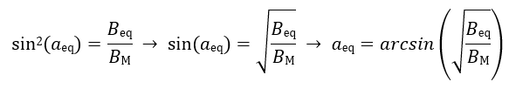
 RSS Feed
RSS Feed