|
Γράφει η Αφροδίτη Νάση και η Πηνελόπη Αγγελοπούλου
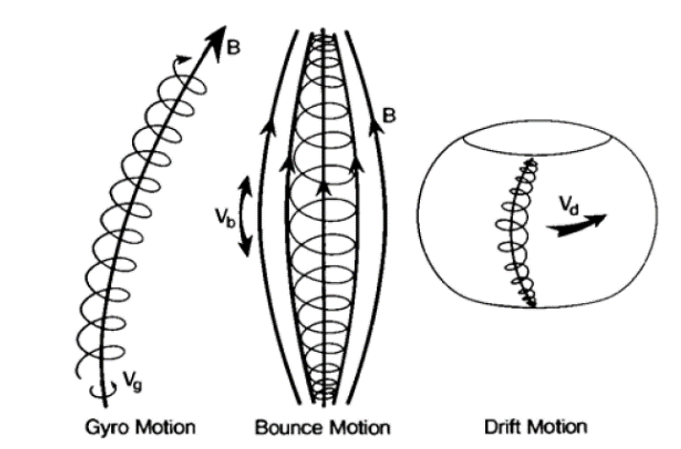
Η γήινη μαγνητόσφαιρα περιέχει διάφορους πληθυσμούς πλάσματος φορτισμένων σωματιδίων, οι οποίοι προέρχονται είτε από τη γήινη ιονόσφαιρα είτε από τον ηλιακό άνεμο (βλέπε και άρθρο 1ου Τεύχους: Παγιδευμένα φορτισμένα σωματίδια γύρω από τη Γη). Οι πληθυσμοί αυτοί αλληλεπιδρούν και επηρεάζουν ταυτόχρονα τις δομές των ηλεκτρικών και μαγνητικών πεδίων, οι οποίες με τη σειρά τους καθορίζουν και την ίδια την κίνηση των σωματιδίων, οδηγώντας τα στο να πραγματοποιούν τις τρεις χαρακτηριστικές κινήσεις τους (Εικόνα 1): τη γυροκίνηση (gyro-motion), την κίνηση αναπήδησης (bounce motion) και την κίνηση ολίσθησης (drift motion). Ποιοι μηχανισμοί όμως οδηγούν σε αυτό το αποτέλεσμα; Σε αυτό το άρθρο θα εξετάσουμε τον τρόπο με τον οποίο ένα φορτισμένο σωματίδιο καταλήγει να εκτελεί γυροκίνηση γύρω από μία μαγνητική δυναμική γραμμή.
Εικόνα 1: Οι τρεις κινήσεις των παγιδευμένων φορτισμένων σωματιδίων μέσα στο μαγνητικό πεδίο. Πηγή: Kivelson & Russel (1995).
QΑς ξεκινήσουμε από την γενικότερη περίπτωση. Έστω ένα φορτισμένο σωματίδιο, το οποίο έχει μάζα m και φορτίο q, και το οποίο κινείται με ταχύτητα και επιτάχυνση , σε περιοχή με μαγνητικό πεδίο και ηλεκτρικό πεδίο . Τότε, στο σωματίδιο θα ασκείται η δύναμη Lorentz:
(όπου το σύμβολο x υποδηλώνει εξωτερικό γινόμενο). Έστω ακόμα ότι το σωματίδιο δέχεται και μια εξωτερική δύναμη F. Τότε, στο σωματίδιο θα ασκείται συνολική δύναμη:
Αντικαθιστώντας τον 2ο νόμο του Νεύτωνα στη σχέση για την δύναμη F προκύπτει η εξίσωση κίνησης:
σύμφωνα με τη λύση της οποία μπορούμε να περιγράψουμε λεπτομερώς την κίνηση του σωματιδίου.
Στη συνέχεια θα αναλύσουμε την πιο απλή περίπτωση εφαρμογής των παραπάνω, και θα δούμε πώς αυτή οδηγεί στην πρώτη από τις τρεις χαρακτηριστικές κινήσεις των σωματιδίων, τη γυροκίνηση. Υποθέτουμε ότι το σωματίδιο κινείται σε περιοχή στην οποία υπάρχει ένα ομογενές και σταθερό μαγνητικό πεδίο B, απουσία ηλεκτρικού πεδίου, Ε=0 . Κάνουμε επιπλέον την υπόθεση ότι δεν ασκείται καμία εξωτερική δύναμη, δηλαδή F=0. Στην περίπτωση αυτή, η δύναμη που δρα στο σωματίδιο είναι:
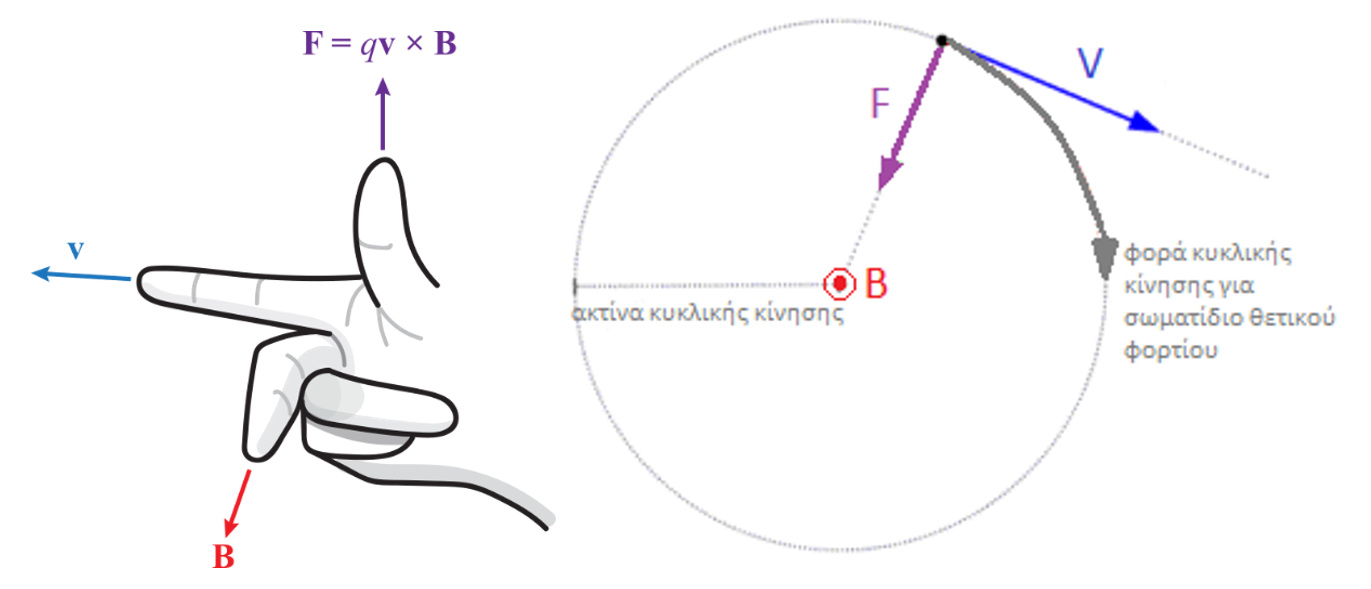
Η δύναμη αυτή έχει διεύθυνση κάθετη στο επίπεδο της ταχύτητας και του μαγνητικού πεδίου (όπως ορίζει το εξωτερικό γινόμενο, το οποίο υπολογίζεται εύκολα με τον κανόνα του δεξιού χεριού (Εικόνα 2)), και η φορά της εξαρτάται από το πρόσημο του φορτίου του σωματιδίου.
Χωρίζουμε την ταχύτητα του σωματιδίου σε δυο συνιστώσες, μια κάθετη (⊥) και μια παράλληλη (∥) στο μαγνητικό πεδίο:
και έτσι έχουμε:
Επομένως, η δύναμη υπό την επίδραση της οποίας κινείται το σωματίδιο (όπως και πάλι ορίζει το εξωτερικό γινόμενο) είναι κάθετη και στο μαγνητικό πεδίο B αλλά και στην κάθετη ταχύτητα V, το οποίο σημαίνει ότι δρα ως κεντρομόλος δύναμη, αναγκάζοντας το σωματίδιο να ακολουθεί κυκλική τροχιά γύρω από το μαγνητικό πεδίο B, με φορά που εξαρτάται από το φορτίο του.
Εικόνα 2: Ο κανόνας του δεξιού χεριού δίνει εύκολα τη φορά της δύναμης Lorentz, γνωρίζοντας τη φορά της ταχύτητας V και του μαγνητικού πεδίου B (στη δεξιά εικόνα αυτό εξέρχεται της σελίδας). Η δύναμη είναι πάντα κάθετη σε αυτά, αλλά η φορά της εξαρτάται από το φορτίο q του σωματιδίου. Για θετικό φορτίο (q>0), ακολουθεί τον αντίχειρα και κινείται δεξιόστροφα γύρω από το πεδίο Β, ενώ για αρνητικό φορτίο (q<0) η φορά του είναι αριστερόστροφη. Στις συγκεκριμένες εικόνες, η ταχύτητα είναι πλήρως κάθετη στο μαγνητικό πεδίο, επομένως απεικονίζεται η V κάθετη. (Πηγή και Πηγή)
Διαπιστώνουμε λοιπόν ότι προκύπτουν δυο επιμέρους κινήσεις τις οποίες εκτελεί το σωματίδιο:
Αυτό σημαίνει ότι τα δυο κύρια είδη φορτισμένων σωματιδίων που αποτελούν τους πληθυσμούς πλάσματος της μαγνητόσφαιρας, δηλαδή τα ηλεκτρόνια και τα πρωτόνια, θα εκτελούν το ίδιο είδος κίνησης, αλλά το καθένα με διαφορετικά χαρακτηριστικά (διαφορετική ακτίνα και αντίθετη φορά κυκλικής κίνησης).
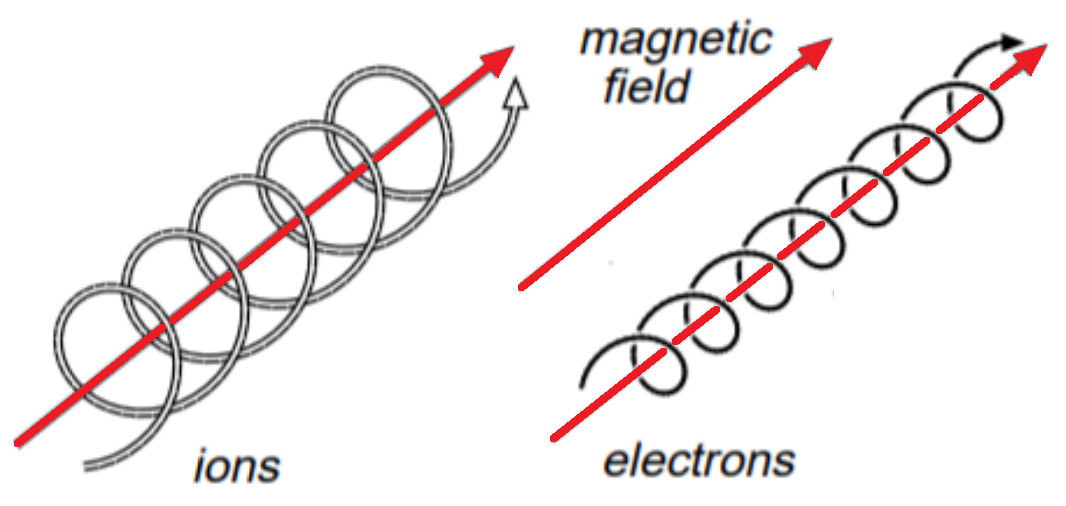
Εικόνα 3: Η γυροκίνηση που εκτελούν τα σωματίδια γύρω από τις δυναμικές γραμμές του μαγνητικού πεδίου. Τα ηλεκτρόνια (μικρή μάζα, αρνητικό φορτίο) έχουν μικρή ακτίνα έλικας και αριστερόστροφη φορά, ενώ τα διάφορα ιόντα και τα πρωτόνια (μεγαλύτερη μάζα, θετικό φορτίο) έχουν μεγαλύτερη ακτίνα και δεξιόστροφη φορά. (Πηγή)
Για ευκολότερη περιγραφή της γυροκίνησης, πολλές φορές η κάθετη ταχύτητα της κυκλικής κίνησης ονομάζεται ‘’γυροταχύτητα’’ ή ‘’ταχύτητα Larmor’’ οπότε και συμβολίζεται με έναν δείκτη L, δηλαδή: Vκάθετη = VL, ενώ η παράλληλη ταχύτητα της ευθύγραμμης κίνησης ονομάζεται ‘’ταχύτητα οδηγού κέντρου’’ και συμβολίζεται με έναν δείκτη gc (από το guiding center): V//=Vgc.
Έτσι, ορίζοντας ως οδηγό κέντρο το κέντρο της κυκλικής τροχιάς, μπορούμε να αναλύσουμε την γυροκίνηση σε δυο επιμέρους κινήσεις, ως εξής:
Εικόνα 4: Ο ορισμός του οδηγού κέντρου ως το κέντρο της κυκλικής κίνησης που εκτελούν τα σωματίδια γύρω από το μαγνητικό πεδίο, και ο διαχωρισμός των κινήσεων στην κίνηση του οδηγού κέντρου (κατά μήκος της μαγνητικής γραμμής), και του πραγματικού σωματιδίου (που κινείται κυκλικά γύρω από το οδηγό κέντρο). (Πηγή και Πηγή)
Ο διαχωρισμός αυτός θα μας φανεί χρήσιμος στη μελέτη των άλλων δύο κινήσεων, αφού θα μας επιτρέψει να μελετήσουμε πιο εύκολα τη συνολική κίνηση ενός σωματιδίου εντός της μαγνητόσφαιρας, λαμβάνοντας υπ’ όψη μόνο την κίνηση του οδηγού κέντρου.
Σε επόμενα άρθρα θα δούμε πώς οι πιο σύνθετες περιπτώσεις οδηγούν στην κίνηση ανάκλασης και στην κίνηση ολίσθησης. Comments are closed.
|

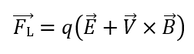
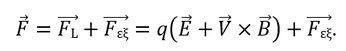
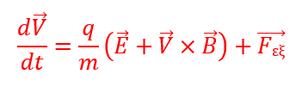
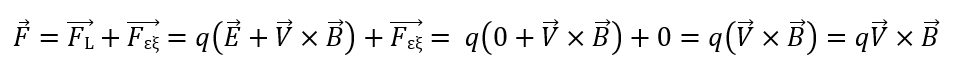
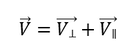
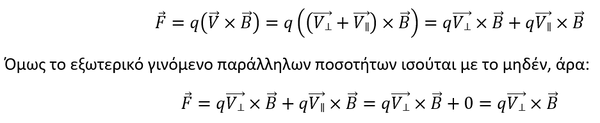

 RSS Feed
RSS Feed