|
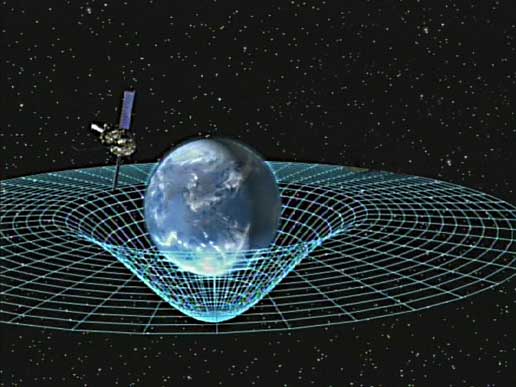
Του Γιώργου Μουζλάνοβ 11 Φεβρουαρίου 2016. Η επιστημονική ομάδα του LIGO και του VIRGO ανακοινώνει πως πέντε μήνες νωρίτερα, στις 14 Σεπτεβρίου 2015, παρατηρήθηκαν άμεσα για πρώτη φορά, βαρυτικά κύματα από τη συγχώνευση δύο μαύρων οπών. 'Εκτοτε, συνεχίζει να ανιχνεύει όλο και περισσότερα γεγονότα. Μάλιστα, την επόμενη χρονιά, το 2017, δόθηκε το βραβείο Nobel στους Rainer Weiss, Kip Thorne και Barry Barish για τη συνεισφορά τους πάνω στην ανίχνευση των βαρυτικών κυμάτων. Ακούγοντας κάποιος αυτή την ειδηση και σκεπτόμενος πως το Nobel εχει δωθεί σε μερικούς μεγάλους επιστήμονες στο παρελθόν (αποφεύγουμε την αναφορά σε ονόματα για να μήν αδικήσουμε κάποιον που μπορεί να ξεχάσουμε, άλλωστε η πλήρης λίστα υπάρχει στην ιστοσελίδα των βραβείων Νόμπελ), προκύπτει ότι μάλλον ειναι κάτι σημαντικό αυτό που ονομάζουμε βαρυτικά κύματα. Τι είναι όμως τα βαρυτικά κύματα, και γιατί έχουν αλλάξει τον τρόπο με τον οποίο βλέπουμε το σύμπαν; Πριν αρχίσουμε να μιλάμε για βαρυτικά κύματα, θα εξετάσουμε πως και γιατί οδηγηθήκαμε σε αυτά. Για τον σκοπό αυτό θα κάνουμε ενα μικρό (και νοητό) ταξίδι στο χρόνο. Προορισμός μας ειναι η Μεγάλη Βρετανία του 1687, χρονιά που ο Isaac Newton εκδίδει το Principia, μέσα απο το οποίο αναπτύσσει την θεώρησή του για την βαρύτητα. Παρουσιάζει τον γνωστό νόμο της παγκόσμιας ελξης που περιγράφει τη δύναμη που ασκείται μεταξύ δύο σωμάτων με μάζα. Μαθηματικά αυτός γράφεται ώς εξής: $$\vec{F}=-G\frac{m_1m_2}{r^2}\hat{r}$$ Την έχουμε γράψει σε διανυσματική μορφή, για να τονίσουμε τον ελκτικό χαρακτήρα της δύναμης με το αρνητικό πρόσημο. G είναι η βαρυτική σταθερά, την οποία την μέτρησε πειραματικά ο Cavendish το 1798 και -πλέον- κάθε πρωτοετής φοιτητής στο Φυσικό Αθήνας. και r ειναι η απόσταση μεταξύ των δύο σωμάτων. Εικόνα 1. Sir Isaac Newton (1642 - 1727). Η εξίσωση αυτή ήταν επιτυχής στο να περιγράψει τις κινήσεις των ουράνιων σωμάτων στο ηλιακό μας σύστημα και να αποδείξει τους γνωστούς για την εποχή νόμους του Kepler. Ωστόσο, παρουσίαζε ορισμένα προβλήματα. Πρώτο και κυριότερο περιγράφει μία δύναμη που ειναι στιγμιαία, και με άπειρη ταχύτητα διάδοσης. Τι σημαίνει αυτό; Σημαίνει πως αν ξαφνικά εμφανιστεί μία μάζα σε κάποιο σημείο του χώρου, όλα τα υπόλοιπα σώματα που βρίσκονται στην εμβέλεια του θα "νιώσουν" αμέσως την δύναμη που τους ασκείται από αυτό. Κάτι τετοιο, εκ πρώτης όψεως, φαντάζει ως παράδοξο, καθώς γνωρίζουμε πως τίποτα δεν μπορεί να μεταδοθεί πιο γρήγορα απο την ταχύτητα του φωτός. Ένα άλλο πρόβλημα ήταν ότι εμφανίζονταν αποκλίσεις στις προβλέψεις της θεωρίας του Newton όταν αρχίσαμε να μελετάμε πιο ακραία περιβάλλοντα βαρύτητας, όπως πολύ κοντά σε ένα άστρο, ή σε πιο μαζικά άστρα απο τον Ήλιο. Για την ώρα θα αφήσουμε αυτά τα ερωτήματα αναπάντητα. Συνεχίζουμε το ταξίδι μας στον χρόνο, μερικούς αιώνες μπροστά και πάμε στο 1915, όπου ο καταξιωμένος πλέον Albert Einstein παρουσιάζει την δική του θεώρηση πάνω στη βαρύτητα που ονομάζεται Γενική Θεωρία της Σχετικότητας (η γενίκευση δηλαδή της Ειδικής θεωρίας της Σχετικότητας που εκδόθηκε το 1905). Μέσα από αυτή, ο Einstein μας λέει πως ο χώρος και ο χρόνος (που έχουν ήδη ενωθεί σε μία οντότητα, τον χωρόχρονο) δεν είναι κάτι στατικό και άκαμπτο, αλλά "καμπυλώνονται" από την μάζα (και την ενέργεια). Mαθηματικά η θεωρία αυτή περιγράφεται από τις λεγόμενες Εξισώσεις Πεδίου του Einstein: $$R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}+\Lambda g_{\mu\nu}=\frac{8\pi G}{c^4}T_{\mu\nu}$$ Όπου c=300.000 km/sec είναι η ταχύτητα του φωτός στο κενό. Ίσως με μία πρώτη ματιά η γραφή αυτή τρομάζει τον αναγνώστη, ωστόσο ας προσπαθήσουμε να καταλάβουμε διαισθητικά τι περίπου περιγράφει η παραπάνω σχέση. Θα ξεκινήσουμε με το δεξί μέλος. Το σύμβολο $$T_{\mu\nu}$$ ονομάζεται τανυστής ενέργειας-ορμής και όπως λέει το όνομά του, μας περιγράφει πως κατανέμεται η ενέργεια-μάζα (κάθε μορφής) στο χώρο. Προχωρώντας στα αριστερά, ο όρος $$R_{\mu\nu}$$ ονομάζεται τανυστής καμπυλότητας του Ricci και μας περιγράφει την γεωμετρία ή την καμπυλότητα του χωρόχρονου (μήν ξεχνάμε πως η ΓΘΣ ειναι μία γεωμετρική θεωρία). Συνεχίζοντας το σύμβολο $$g_{\mu\nu}$$ ονομάζεται μετρικός τανυστής (ή σκέτο μετρική) και στην ουσία είναι ο χαρακάς μας για να μετράμε αποστάσεις στο σύμπαν. Το $$\Lambda$$ ονομάζεται κοσμολογική σταθερά, αλλά σε πρώτη προσέγγιση δεν μας απασχολεί αυτός ο όρος. Η λύση της αρχικής εξίσωσης μας δίνει τη μετρική. Έχοντας δηλαδή γνώση για την ύλη (τανυστής ενέργειας-ορμής) και για την καμπυλότητα (τανυστής Ricci) βρίσκουμε πως αλλάζει η μεζούρα μας. Υπό αυτή την έννοια προκύπτει και η φράση που πιθανόν έχετε ακούσει, ότι η ύλη λέει στο χώρο πως να καμπυλωθεί (πηγαίνοντας απο τα δεξιά προς τα αριστερά στην εξίσωση) και πως η καμπύλωση μαρτυρά την παρουσία μάζας ή ενέργειας εν γένει (κοιτώντας την εξίσωση από αριστερά προς τα δεξιά). Μία επιβεβαίωση πως η ΓΘΣ είναι η σωστή θεωρία για την βαρύτητα είναι πως παίρνοντας το όριο "ασθενούς" βαρύτητας καταλήγουμε στη θεωρία του Newton για τη βαρύτητα που είδαμε νωρίτερα. Εικόνα 2. Η καμπύλωση του χωρόχρονου παρουσία μάζας. Πηγή: LIGO Το νέο αυτό πρίσμα υπό το οποίο βλέπουμε την βαρύτητα, κατάφερε να εξηγήσει όλα εκείνα τα σημεία στα οποία η θεωρία του Newton απέτυχε. Επαληθεύτηκε πειραματικά στα επόμενα χρόνια και συνεχίζει ακόμα και σήμερα να επαληθεύει κάθε θεωρητικό της αποτέλεσμα. Επομένως, είμαστε πεπεισμένοι πως η Γενική Θεωρίας της Σχετικότητας είναι η σωστή θεωρία για να περιγράψουμε τη βαρύτητα. Ο τρόπος με τον οποίο ο Einstein έλυσε το πρόβλημα της στιγμιαίας δύναμης από απόσταση, ήταν με την εισαγωγή των βαρυτικών κυμάτων που μεταδίδονται με την ταχύτητα του φωτός. Τα βαρυτικά κύματα προκύπτουν λύνοντας την παραπάνω εξίσωση με τον πιο τεχνικό τρόπο της Γραμμικοποιημένης Βαρύτητας. Για να καταλάβουμε τι επιπλοκές έχει η πεπερασμένη ταχύτητα της βαρύτητας, ας σκεφτούμε το εξής παράδειγμα: αν ξαφνικά για κάποιο λόγο ο Ήλιος εξαφανιζόταν, στη Γη η πληροφορία αυτή θα έπαιρνε γύρω στα 8 λεπτά για να μας φτάσει (όσο χρόνο κάνει δηλαδή και το φώς για να ταξιδέψει από τον Ήλιο στη Γη). Μέχρι εκείνη τη στιγμή, θα βλέπαμε και θα αισθανόμασταν βαρυτικά, την επίδραση του και θα γυρίζαμε γύρω απο αυτόν σαν να ήταν ακόμα εκεί. Τι είναι όμως τα βαρυτικά κύματα; Θα ξεκινήσουμε κοιτάζοντας τις δύο λέξεις που τα απαρτίζουν ξεχωριστά. Όταν ακούμε την λέξη κύματα, το πρώτο πράγμα που μας έρχεται διαισθητικά στο νου, είναι τα κύματα στην επιφάνεια της θάλασσας, σκέψη που δεν είναι λάθος. Στην ουσία τα κύματα είναι μια διαταραχή σε ένα μέσο. Εάν δεν υπάρχει κάτι να διαταράξει το μέσο μας, τότε θα βλέπουμε μία ήρεμη επιφάνεια (στη περίπτωση μιας λίμνης). Αν όμως για παράδειγμα ρίξουμε μία πέτρα, θα δούμε ξαφνικά να εμφανίζονται διαταραχές ή αλλιώς κύματα από το σημείο στο οποίο ρίξαμε την πέτρα και οι οποίες ταξιδεύουν προς όλες τις διευθύνσεις πάνω στην επιφάνεια. Η ίδια αρχή ισχύει σε κάθε είδους κύμα. Ο επιθετικός προσδιορισμός μπροστά από την λέξη κύματα, μας υποδηλώνει την φύση του φαινομένου που εξετάζουμε. Προφανώς τα υδάτινα κύματα δεν είναι τα μόνα που συναντώνται στη φύση, έτσι υπάρχουν τα ηλεκτρομαγνητικά κύματα, τα κύματα πυκνότητας (ηχητικά), τα βαρυτικά (στα οποία εστιάζουμε στο παρόν άρθρο) κ.α. Εικόνα 3. Κυματισμοί στην επιφάνεια μιάς λίμνης. Πηγή: LIGO Στην περίπτωση των υδάτινων κυμάτων ξέρουμε ήδη πως να τα παράξουμε, από μικρή ηλικία, όλοι μας έχουμε παίξει πετώντας πέτρες στη θάλασσα. Αν όμως άντι για μία υδάτινη επιφάνεια έχουμε τον χωρόχρονο, πώς τον διαταράσσουμε κατ' αναλογία με όσα ήδη ξέρουμε; Για να χτίσουμε την διαίσθηση μας περισσότερο, θα χρησιμοποιήσουμε το απλουστευμένο μοντέλο του "ελαστικού σεντονιού" όπου μπορούμε να φανταστούμε τον χώρο σαν μία δισδιάστατη ελαστική επιφάνεια (όπως αυτή ενός τραμπολίνο). Τι θα συμβεί αν τοποθετήσουμε μία μπάλα σε κάποιο σημείο αυτού του σεντονιού; Οπως πολύ σωστά μαντέψατε, θα δημιουργηθεί ένα βαθούλωμα ή αλλιώς, μία καμπύλωση. Είναι όμως αυτό αρκετό για να δημιουργηθούν βαρυτικά κύματα; Δηλαδή είναι ικανή και μόνο η παρουσία μάζας στον χώρο να παράξει διαταραχές; Η απάντηση είναι όχι. Σκεφτείτε όμως την περίπτωση που εμείς πάρουμε αυτή τη μπάλα και αρχίζουμε να την κουνάμε είτε επιταχύνοντας την είτε αλλάζοντας της διεύθυνση, πάνω στο σεντόνι. Ξαφνικά θα δούμε,πως καθώς μετακινείται, εμφανίζονται ρυτιδώσεις ή αλλιώς τα πολυπόθητα βαρυτικά κύματα που ψάχνουμε. Άρα έχουμε καταφέρει να βρούμε, επί της αρχής, το αίτιο που προκαλεί την δημιουργία τους. Και αυτό δεν είναι άλλο από την επιτάχυνση των σωμάτων. Ας μελετήσουμε όμως τους μηχανισμούς που κρύβονται πίσω από την παραγωγή τους λίγο καλύτερα. Συνεχίζουμε με το παράδειγμα της μπάλας στο ελαστικό μας σεντόνι. Αν αρχίσουμε να περιστρέφουμε αυτή τη σφαίρα γύρω από τον εαυτό της, το "βαθούλωμα" δεν θα αλλάξει. Επομένως δεν θα παραχθούν διαταραχές. Αν όμως η μπάλα μας, αντί για το τέλειο σφαιρικό σχήμα που είχε μέχρι τώρα, έμοιαζε περισσότερο με μία μπάλα του ράκμπι κι αυτή περιστρεφόταν όχι γύρω από τον άξονα συμμετρίας της, τότε αυτή η διαφορά στο σχήμα της θα ήταν ικανή να δημιουργήσει ρυτιδώσεις πάνω στο σεντόνι. Άρα καταλήγουμε στο συμπέρασμα πως αποκλίσεις από το σφαιρικό σχήμα ενός αντικειμένου (εφόσον αυτό επιταχύνεται) οδηγούν στην παραγωγή βαρυτικών κυμάτων. Στο ίδιο αποτέλεσμα θα φτάναμε και αν είχαμε "φούσκωμα-ξεφούσκωμα" της μπάλας μας, με σφαιρικό ή όχι σχήμα. Σε πιο τεχνικό επίπεδο, τα παραπάνω είναι μία συνέπεια του θεωρήματος του Birkhoff, ωστόσο δεν θα επεκταθούμε παραπάνω σε αυτό. Από την σκοπιά της αστροφυσικής, η προηγούμενη ανάλυση μεταφράζεται ως εξής: ένα στατικό σφαιρικό άστρο δε δημιουργεί βαρυτικά κύματα, όπως δε δημιουργεί και στην περίπτωση που το εν λόγω άστρο απλά περιστρέφεται γύρω από τον εαυτό του. Αν όμως εμφανίζεται κάποιο εξόγκωμα στην επιφάνεια του και επιπλέον υπάρχει περιστροφή, όπως συμβαίνει στην περίπτωση ορισμένων άστρων νετρονίων, τότε θα έχουμε παραγωγή βαρυτικών κυμάτων. Το ίδιο συμβαίνει και αν έχουμε κάποιο κατακλυσμιαίο γεγονός, όπως μία έκρηξη σουπερνόβα, όπου είναι εξαιρετικά σπάνιο αυτό να είναι πλήρως συμμετρικό σε όλες τις διευθύνσεις. Προχωράμε τώρα σε ένα άλλο σενάριο. Ας σκεφτούμε πως αντί για μία μπάλα, έχουμε δύο πλέον μπάλες και είναι ενωμένες με μία αρκετά λεπτή και αμελητέας μάζας ράβδο, σαν ένα βαράκι. Αν αυτή η διάταξη περιστρέφεται γύρω από τον άξονα συμμετρίας της και πάλι δεν θα έχουμε κάποια διαταραχή. Όμως αν η περιστροφή είναι κάθετη στη ράβδο που τα ενώνει, τότε θα παρατηρήσουμε πως δημιουργούνται βαρυτικά κύματα και μάλιστα όσο πιο κοντά πλησιάζουν οι δυο σφαίρες, τόσο πιο έντονο θα είναι το φαινόμενο, μέχρις ότου φτάσουν αρκετά κοντά ώστε να συγχωνευτουν.Το αστροφυσικό ανάλογο είναι ένα διπλό σύστημα, που συνήθως αποτελείται από αστέρες νετρονίων και μαύρες τρύπες σε οποιονδήποτε συνδυασμό αυτών. Σημαίνει αυτό όμως πως δεν παράγονται βαρυτικά κύματα και από άλλα αντικείμενα στο σύμπαν; Όπως για παράδειγμα ένα άστρο και τον πλανήτη που περιστρέφεται γύρω από αυτόν; Η απάντηση είναι πως ναι, παράγονται, ωστόσο αυτά είναι τόσο ασθενή που η ύπαρξη τους, όσο και η ανίχνευση τους, ουσιαστικά δεν εχουν καμία σημασία στην ευρύτερη μελέτη του συστήματος. Με το ίδιο σκεπτικό, αν αρχίσετε να γυρίζετε γύρω από τον εαυτό σας με ανοιχτά τα χέρια, θα παράξετε βαρυτικά κύματα, μη περιμένετε όμως κάποια εμφανή διαφορά στον περιβάλλοντα χώρο σας. Το πιο πιθανό είναι πως ίσως ιδρώσετε λίγο. Εικόνα 4. Παραγωγή βαρυτικών κυμάτων από διπλό σύστημα μαζών. Πηγή: Rochester Institute of Technology. Ας πάμε τώρα να κάνουμε λίγη φυσική (γιατί μέχρι τώρα κουνούσαμε απλά τα χέρια μας και παράγαμε βαρυτικά κύματα). Μέσα από τη μελέτη του φορμαλισμού των βαρυτικών κυμάτων κάποιος μπορεί να καταλήξει στις δυο παρακάτω σχέσεις: $$L_{GW}=\frac{dE}{dt}=\frac{1}{5}\frac{G}{c^5}\langle\dddot Q_{jk}\dddot Q_{jk}\rangle$$ $$h_{jk}=\frac{2}{r}\frac{G}{c^4}\ddot{Q}_{jk}(t-\frac{r}{c})$$ Η πρώτη μας περιγράφει την ενέργεια που ακτινοβολεί (και κατά συνέπεια χάνει) η πηγή μέσω αυτού και η δεύτερη το πλάτος του κύματος. Το σύμβολο Qjk ονομάζεται τετραπολική ροπή, για την ώρα δείτε το σαν μία ιδιότητα (όπως είναι η μάζα ή το φορτίο) που περιγράφει ένα σώμα. Οι τελείες από πάνω συμβολίζουν χρονικές παραγώγους, ενώ οι αγκύλες σημαίνουν μέση τιμή. Για να τις μελετήσουμε θα κάνουμε την λεγόμενη εκτίμηση τάξης μεγέθους, δηλαδή πόσο μεγάλη (ή μικρή) περιμένουμε να είναι αυτή η ποσότητα. Για το μεν πλάτος βρίσκουμε πως: $$h\sim\frac{r_s}{r}\frac{v^2}{c^2}$$ όπου rs είναι η ακτίνα του Schwarzschild και δίνεται από τον τύπο $$r_s=2\frac{GM}{c^2}$$ Κάποιοι ίσως την έχουν ακούσει να περιγράφει τον ορίζοντα γεγονότων στην περίπτωση των μαύρων τρυπών, ωστόσο μη μπερδευτείτε, δεν θα ασχοληθούμε με αυτή την έννοια, απλώς μας βολεύει να γράφουμε πιο συνεπτυγμένα τις εξισώσεις μας και γιατί μπορούμε να συγκρίνουμε πιο εύκολα την ακτίνα των αντικειμένων που μελετάμε. r είναι η απόστασή μας από την πηγή του κύματος. Ενώ για την λαμπρότητα: $$L_{GW}\sim\frac{c^5}{G}\Big(\frac{r_s}{R}\Big)^2\Big(\frac{v}{c}\Big)^6$$ Ο "περίεργος" αναγνώστης μπορεί να αντικαταστήσει τις αριθμητικές τιμές και να υπολογίσει το πλάτος και πόση ενέργεια θα χάνει με την εκπομπή βαρυτικών κυμάτων αν αρχίσει να περιστρέφεται γύρω από τον εαυτό του. Μία πρώτη και άμεση παρατήρηση είναι πως και οι δύο αυτές ποσότητες παίρνουν αρκετά μεγάλες τιμές (και άρα ανιχνεύσιμες) όταν εξετάζουμε συστήματα όπου οι διαστάσεις τους είναι $$R\sim r_s$$ και οι ταχύτητες $$v\sim c$$ όπου οι συνθήκες αυτές ικανοποιούνται στα συμπαγή αντικείμενα (αστέρες νετρονίων και μαύρες τρύπες). Κάποιος θα μπορούσε να σκεφτεί, γιατί μας ενδιαφέρει όμως το πλάτος του κύματος; Βίντεο 1. Συγχώνευση μελανών οπών. Πηγή: LIGO Ας επιστρέψουμε πίσω στην αναλογία των υδάτινων κυμάτων για να το καταλάβουμε διαισθητικά. Όταν έχουμε ένα κύμα στην επιφάνεια της θάλασσας, αυτό που παρατηρούμε είναι μία αυξομείωση στη στάθμη του νερού. Αν τοποθετήσουμε μία σημαδούρα, θα δούμε πως αυτή θα αρχίσει να ανεβοκατεβαινει. Όσο μεγαλύτερο το κύμα (σε πλάτος) τόσο πιο μεγάλη η μετατόπιση της. Κάτι αντίστοιχο συμβαίνει και στη περίπτωση των βαρυτικών κυμάτων, μόνο που τώρα αντί για τη αυξομείωση στο ύψος της θάλασσας, έχουμε την αυξομείωση στο μήκος του χώρου. Δηλαδή αν σκεφτούμε πως έχουμε ένα χάρακα και μέσα από αυτόν περνάει ένα βαρυτικό κύμα, αυτό που θα συμβεί είναι πως ο χάρακας θα μεγαλώσει και θα μικρύνει κατά τη διάρκεια του γεγονότος. Ωστόσο μην τρομάξετε, τα βαρυτικά κύματα είναι εξαιρετικά ασθενή και η αλλαγή που επιφέρουν είναι σχεδόν (αλλά όχι εντελώς) ανεπαίσθητη. Για να καταλάβουμε πόσο "αδύναμα" είναι ας σκεφτούμε πως έχουμε μία έκρηξη supernova στο γαλαξιακό σμήνος της Παρθένου (100 εκατομμύρια έτη φωτός μακριά) και η ενέργεια που εκλύεται είναι της τάξης των $$10^{-4}M_\odot$$ (θυμηθείτε πως η ενέργεια είναι ισοδύναμη με τη μάζα από τη διάσημη σχέση E=mc^2), με συχνότητα f=1kHz και το σήμα μας έχει διάρκεια 1 msec. Σε αυτή τη περίπτωση το πλάτος του κύματος που θα ανιχνεύσουμε εμείς στη Γή θα δίνεται από τη σχέση: $$h\approx 10^{-22}\Big(\frac{E_{GW}}{10^{-4}M_\odot}\Big)^{1/2}\Big(\frac{1}{1kHz}\Big)^{-1}\Big(\frac{\tau}{1msec}\Big)^{-1/2}\Big(\frac{r}{15Mpc}\Big)^{-1}$$ Επομένως, άμα σκεφτούμε πως ο "χάρακας" μας(που ονομάζεται συμβολόμετρο) έχει μήκος 4 km η αλλαγή που θα παρατηρήσουμε θα είναι: $$\Delta l=h\cdot l=10^{-22}4km=4\times 10^{-17}cm$$ Εικόνα 5. Ο ανιχνευτής VIRGO στην Πίζα της Ιταλίας. Πηγη: VIRGO Για να καταλάβουμε πόσο μικρό είναι αυτό το νούμερο, ας θυμηθούμε πως ενα τυπικό μέγεθος για τα άτομα είναι της τάξης του 10^-8 cm. Οπότε βλέπουμε, πόσο ασθενή είναι τα βαρυτικα κύματα, ακόμα και από τις πιο έντονες πηγές στο σύμπαν και γιατί ακόμα και ο ίδιος ο Einstein θεωρούσε πως δεν θα ήταν δυνατή η ανίχνευση τους. Παρόλα αυτά αν και χρειάστηκε να περάσουν 100 χρόνια από τότε που θεμελιώθηκε η θεωρία και χάρις στην πρόοδο της τεχνολογίας και την επιμονή του ανθρωπίνου πνεύματος, καταφέραμε το φαινομενικά αδύνατο. Μέχρι τώρα,μελετήσαμε τι είναι τα βαρυτικά κύματα,και πώς παράγονται. Ωστόσο ακόμα δεν απαντήσαμε ένα πολύ σημαντικό ερώτημα. Γιατί είναι τόσο σημαντικά ώστε να αξίζουν την απονομή 2 βραβείων Nobel (το πρώτο δόθηκε το 1993 στους Hulse και Taylor για την έμμεση ανίχνευση τους); Μέχρι τώρα, όση πληροφορία λαμβάναμε από το σύμπαν, ήταν μέσω ηλεκτρομαγνητικής ακτινοβολίας, δηλαδή φως που έρχεται στα τηλεσκόπια μας (σε κάθε μήκος κύματος). Τα βαρυτικά κύματα όμως, είναι μία εντελώς διαφορετικής φύσεως ακτινοβολία, οπότε η πληροφορία που παίρνουμε είναι εντελώς διαφορετική. Οι συχνότητες στις οποίες εκπέμπεται είναι αρκετά κοντά στις ηχητικές. Επομένως, για μερικές χιλιάδες χρόνια, από τότε που ο άνθρωπος έστρεψε τα μάτια του στον έναστρο ουρανό, είχαμε μόνο την αίσθηση της όρασης να μας βοηθάει στην κατανόηση του σύμπαντος. Πλέον όμως, θα μπορούσε να πει κάποιος, ότι έχουμε "εξελιχθεί" και έχουμε αναπτύξει ένα ακουστικό όργανο που μας επιτρέπει να ακούμε. Ή αν θέλουμε μία διαφορετική παρομοίωση, εμπνευσμένη απο τις τέχνες, μέχρι τώρα πηγαίναμε στον κινηματογράφο και βλέπαμε βουβές ταινίες του Chaplin και ξαφνικά για πρώτη φορά προβάλλεται ο Μέγας Δικτάτορας (για όσους δεν γνωρίζουν ήταν η πρώτη ταινία στην οποία μίλησε ο Chaplin) και είμαστε σε θέση πλέον να βλέπουμε αλλά και να ακούμε τους ηθοποιούς να μιλάνε. Θα ήθελα να ευχαριστήσω τον καθηγητή και μέντορα μου, Θεοχάρη Αποστολάτο, για την κριτική ανάγνωση και επιβεβαίωση της επιστημονικής ορθότητας του τελικού κειμένου, καθώς και για τα κριτικά του σχόλια πάνω σε αυτό. Πηγές (ή αλλιώς, Τι με κάνει να ειμαι σίγουρος για όσα γράφω)
Comments are closed.
|





 RSS Feed
RSS Feed