|
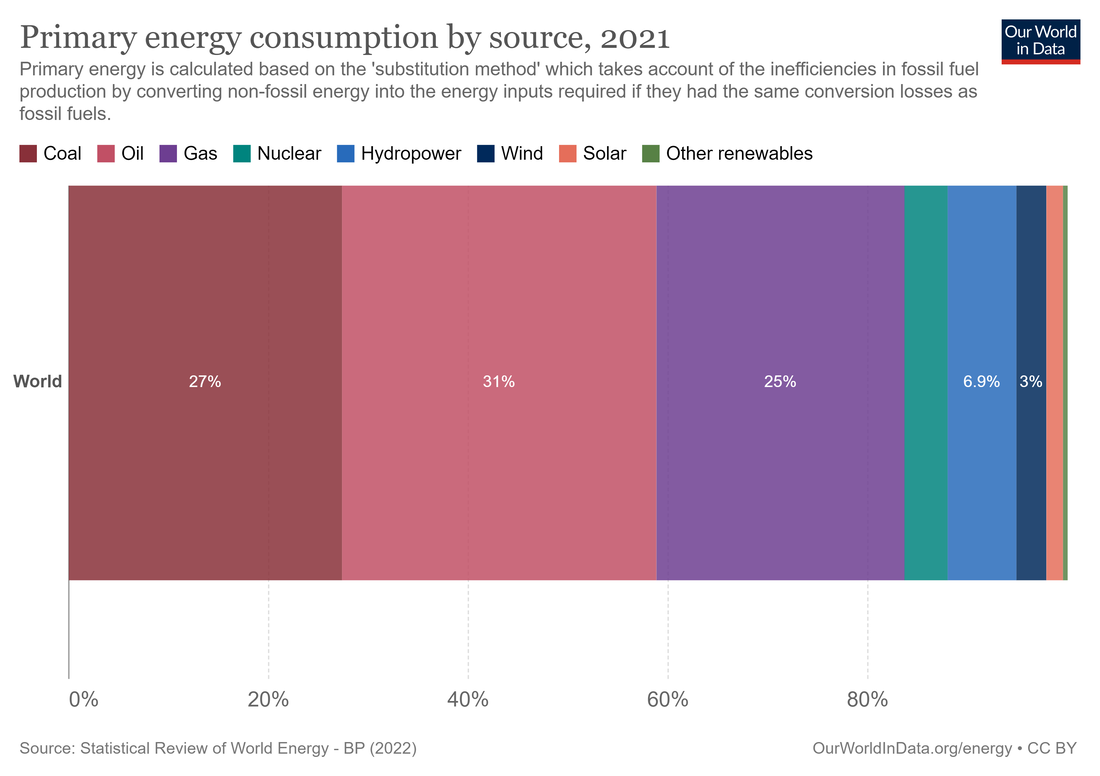
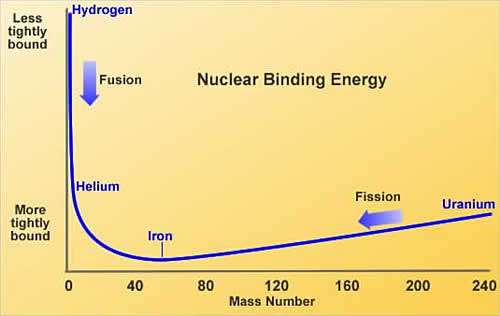
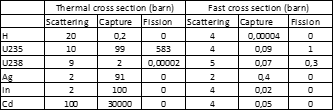
Του Δημήτρη Δημόπουλου Εικόνα εξωφύλλου. Ένας δίσκος ημικατεργασμένου ουρανίου (Πηγή: Office of Nuclear Energy) Η ανακάλυψη της Πυρηνικής Ενέργειας Η πυρηνική ενέργεια ήταν ένας άγνωστος μηχανισμός παραγωγής ενέργειας για τον άνθρωπο, μέχρι τις αρχές του 20ου αιώνα. Αναμφίβολα, ο ίδιος ο πλανήτης μας και κάθε μορφή ζωής που γεννήθηκε και επιβιώνει σε αυτόν, διαμορφώθηκαν χάρις στην πυρηνική ενέργεια που παράγεται άφθονη στον πυρήνα του Ήλιου. Παρόλο όμως που το ηλιακό φως και η ζέστη του είναι κάτι άφθονο και δεδομένο για την ανθρωπότητα, στα πρώτα στάδια επιστημονικής και τεχνολογικής εξέλιξης των ανθρώπινων κοινωνιών, οι μόνοι τρόποι παραγωγής ή μετατροπής ενέργειας που μπορούσαν οι άνθρωποι να χρησιμοποιήσουν, ήταν από δευτερογενείς πηγές κυρίως μηχανικής ή χημικής φύσης. Ο δυνατός αέρας έσπρωχνε ιστιοφόρα καράβια, ο ορμητικός ποταμός έθετε σε περιστροφή τους νερόμυλους, η καύση υλικών παρήγαγε θερμότητα κτλ. Με την ανακάλυψη του ηλεκτρισμού, η ηλεκτρική ενέργεια προστέθηκε στον ανθρώπινο πολιτισμό ως ένας εξαιρετικά χρήσιμο εργαλείο ενεργειακής μεταφοράς. Ένα τεράστιο πλήθος οικιακών και βιομηχανικών συσκευών, δε χρειάζονταν πλέον χειροκίνηση ή αυτόνομους καυστήρες και κινητήρες, αλλά μπορούσαν να λειτουργήσουν με ένα καλώδιο που θα συνέδεε το εργοστάσιο παραγωγής ηλεκτρικής ενέργειας με τον τόπο κατανάλωσης της. Η ίδια η παραγωγή όμως της ηλεκτρικής ενέργειας και της μηχανικής ενέργειας γενικότερα (κίνηση οχημάτων, πλοίων κτλ) βασίστηκε στις παλιές «πρωτόγονες» γνωστές μεθόδους. Κι αυτό εξακολουθεί μέχρι σήμερα. Το 2023, η κατανάλωση πρωτογενούς ενέργειας παγκοσμίως, βασίζεται σε ποσοστό 83% στην καύση υδρογονανθράκων (Εικόνα 1-1). Εικόνα 1-1: Πρωτογενής ενεργειακή κατανάλωση ανά πηγή, 2021. (πηγή: Our World in Data) Η καύση δεν είναι παρά μία χημική αντίδραση. Η ενέργεια προέρχεται από τη λύση χημικών δεσμών που κατά κανόνα είναι εξώθερμες χημικές διαδικασίες. Αλλά αυτή η αντίδραση έχει ένα πολύ μικρό ενεργειακό όφελος σε σχέση με τη μάζα των υλικών που συμμετέχουν στην αντίδραση. Πχ για να βράσουμε μία κατσαρόλα με νερό, χρειάζεται να «κάψουμε» 50ml πετρελαίου. Αν αναλογιστεί κανείς πόσες κατσαρόλες με νερό ζεσταίνονται καθημερινά, καταλαβαίνει ότι χρειάζονται θάλασσες πετρελαίου για να παραχθεί η απαραίτητη ενέργεια μόνο για το ημερήσιο μαγείρεμα. Υπάρχει όμως ένας πολύ πιο αποδοτικός τρόπος να δημιουργηθεί ένα τεράστιο ποσό ενέργειας. Αυτός ο τρόπος πηγάζει στις πιο βαθιές δομές της ύλης, πέρα από τους μοριακούς δεσμούς: στον ίδιο τον πυρήνα των ατόμων. Κάθε στοιχείο που υπάρχει στο σύμπαν, αποτελείται από έναν συγκεκριμένο αριθμό πρωτονίων που ονομάζουμε ατομικό αριθμό. Αν προσθέσουμε η αφαιρέσουμε πρωτόνια από έναν πυρήνα, δημιουργούμε ένα άλλο στοιχείο. Μαζί με τα πρωτόνια, στον πυρήνα του κάθε ατόμου βρίσκονται συνήθως και παραπλήσιος αριθμός νετρονίων. Αλλάζοντας τον αριθμό των νετρονίων δεν δημιουργούμε άλλο στοιχείο (αφού ο ατομικός αριθμός παραμένει ο ίδιος) αλλά άλλο ισότοπο του ίδιου στοιχείου. Για να ξεχωρίζουμε τα ισότοπα μεταξύ τους, χρησιμοποιούμε τον μαζικό αριθμό του ατόμου, που ορίζεται ως το άθροισμα πρωτονίων και νετρονίων στον πυρήνα του. Τα ισότοπα 235U και 238U του ουρανίου, έχουν προφανώς ίδιο ατομικό αριθμό (92) αλλά διαφορετικό αριθμό νετρονίων που μπορεί να υπολογιστεί με μια απλή αφαίρεση. Θα περίμενε κανείς να μπορούμε να υπολογίσουμε κι εύκολα την μάζα του πυρήνα του κάθε ισοτόπου, αν γνωρίζουμε απλά τον ατομικό και μαζικό αριθμό του και τη μάζα του πρωτονίου και του νετρονίου. Όπως όμως διαπιστώθηκε στα τέλη του 19ου αιώνα, η μάζα ενός πυρήνα είναι πάντα μικρότερη από το άθροισμα των πρωτονίων και των νετρονίων που τον αποτελούν! Αυτό το «έλλειμα μάζας» μπορεί να μεταφραστεί σε ενέργεια μέσω της εξίσωσης του Einstein, E=mc^2. Κάθε πυρήνας λοιπόν, με εξαίρεση τον πυρήνα του Η, χαρακτηρίζεται από ένα ποσό ενέργειας που υπολείπεται από το συνολικό ποσό ενέργειας που θα έπρεπε να έχει βάσει των συστατικών του. Αν με μία πυρηνική αντίδραση, από τον αρχικό πυρήνα προκύψει ένας πυρήνας με μεγαλύτερο έλλειμα μάζας, τότε αυτή η μάζα που χάνεται κατά τη μετατροπή, θα αποδοθεί στο περιβάλλον ως ενέργεια. Ξεκινώντας από το Η και πηγαίνοντας σε μεγαλύτερους πυρήνες, το έλλειμα μάζας αυξάνεται. Άρα σε κάθε σκαλοπάτι απελευθερώνεται ενέργεια. Αν δύο 2Η δημιουργήσουν έναν πυρήνα 4He, αυτός θα είναι ελάχιστα πιο ελαφρύς και κατά τη δημιουργία του θα απελευθερωθεί ενέργεια. Αντίστοιχα αν από βαρέα στοιχεία όπως το U, πάρουμε, με διάσπαση, ελαφρύτερους πυρήνες, αυτοί οι πυρήνες θα έχουν ελάχιστα μικρότερη συνολική μάζα άρα πάλι θα απελευθερωθεί ενέργεια. Και οι δύο κλάδοι, από τα ελαφρύτερα προς τα βαρύτερα και από τα βαρύτερα προς τα ελαφρύτερα, συγκλίνουν στο στοιχείο του σιδήρου. Το ισότοπο 56Fe (σίδηρος) έχει το μεγαλύτερο έλλειμα μάζας από όλα τα γνωστά στοιχεία της φύσης. Τα στοιχεία με μικρότερο ατομικό αριθμό από τον σίδηρο, απελευθερώνουν ενέργεια μέσω της πυρηνικής σύντηξης (fusion) ενώ τα στοιχεία με μεγαλύτερο ατομικό αριθμό από τον σίδηρο, πρέπει να διασπώνται με πυρηνική σχάση (fission) (Εικόνα 1-2). Εικόνα 1-2: Οι κλάδοι σύντηξης και σχάσης για την παραγωγή πυρηνικής ενέργειας (Πηγή: ΙΑΕΑ) Lise Meitner και Otto Frisch Η ανακάλυψη της σχάσης του ουρανίου έγινε το 1938 από δύο Αυστριακούς φυσικούς, την Lise Meitner και τον ανιψιό της Otto Frisch σε μία χριστουγεννιάτικη συνάντηση τους στη Σουηδία, όπου η Meitner είχε καταφύγει εξαιτίας της εβραϊκής καταγωγής της. Μετά την ανακάλυψη του νετρονίου, το 1932, οι φυσικοί στα μεγάλα πανεπιστήμια της εποχής, βρήκαν έναν ενδιαφέροντα τρόπο να πειραματίζονται με ατομικούς πυρήνες, χτυπώντας τους με νετρόνια. Στα πειράματα αυτά πρωτοστάτησε ο Ενρίκο Φέρμι, διάσημος επιστήμονας της εποχής και αργότερα νομπελίστας. Τα αποτελέσματα των κρούσεων είχαν περίεργα αποτελέσματα στην περίπτωση βομβαρδισμού εξαιρετικά βαρέων πυρήνων όπως αυτός του ουρανίου. Παρόλο που αρχικά πίστευαν ότι ο βομβαρδισμός ουρανίου με νετρόνια θα είχε ως αποτέλεσμα τη δημιουργία στοιχείων με ατομικό αριθμό μεγαλύτερο του ουρανίου, τα προϊόντα είχαν συμπεριφορά στοιχείων με… μικρότερο ατομικό αριθμό. Όταν ένα από αυτά τα προϊόντα αναγνωρίστηκε ως το μέταλλο Βάριο (Ba) αμέσως θεωρήθηκε κάποιο είδους λάθος μέτρησης. Όμως η Meitner δείχνοντας εμπιστοσύνη στους πειραματικούς συναδέλφους της, προσπάθησε να εξηγήσει με ποιον μηχανισμό μπορεί ένας πυρήνας ουρανίου να μεταστοιχειωθεί στον πολύ ελαφρύτερο πυρήνα βαρίου. Γνωρίζοντας τη μάζα ενός πυρήνα ουρανίου, επεξεργάστηκε την ιδέα, αυτός να διασπάται σε δύο θυγατρικούς πυρήνες που θα αριθμούσαν τον ίδιο συνολικό αριθμό πρωτονίων. Οι συνδυασμοί θα μπορούσαν να είναι πολλοί. Θα μπορούσε να παραχθεί ένα ζευγάρι Στρόντιου (Sr) και Ξένου (Xe) ή Βάριου (Ba) και Κρυπτού (Kr) και μαζί τους 2 ή 3 ταχέα νετρόνια. Όποιος κι αν ήταν όμως ο συνδυασμός των αναμενόμενων προϊόντων, η συνολική τους μάζα θα ήταν μικρότερη κατά το 1/5 της μάζας ενός πρωτονίου από την αρχική μάζα του ουρανίου και του νετρονίου που προσέκρουσε πάνω του. Αυτό το 1/5 της μάζας του πρωτονίου θα αντιστοιχούσε (χρησιμοποιώντας τη διάσημη εξίσωση του Einstein) σε απελευθέρωση ενέργειας ίσης με 200 περίπου MeV ανά σχάση, 82 εκατομμύρια φορές μεγαλύτερη από την καύση υδρογόνου, ένα τρομερό ποσό ενέργειας που όμοιο του δεν είχε κανένας επιστήμονας διανοηθεί ότι μπορούσε να παραχθεί από ένα μόνο άτομο. Το πρόβλημα της κρισιμότητας Η εξήγηση της σχάσης του ουρανίου οδήγησε τον Ενρίκο Φέρμι σε έναν φρενήρη αγώνα να κατασκευάσει μία διάταξη παραγωγής ενέργειας που θα ήταν δυνατό να χρησιμοποιηθεί στη βιομηχανία. Ο Φέρμι προσπάθησε να εφεύρει τον πρώτο πυρηνικό αντιδραστήρα που θα μπορούσε να αυτοσυντηρείται, θα μπορεί δηλαδή να παράγει με σχάση ίδιο αριθμό νετρονίων με αυτά που διαρρέουν ή απορροφώνται από τα υλικά του έτσι ώστε να μη σβήνει αλλά να μην οδηγείται και σε υπερθέρμανση ή ακόμα χειρότερα σε έκρηξη. Αν μπορούσε να επιτευχθεί το ισοζύγιο αυτό, ο αντιδραστήρας θα είχε κρισιμότητα (k) ίση με 1 και δε θα χρειαζόταν εξωτερική πηγή νετρονίων παρά μόνο κατά την έναρξη λειτουργίας του. Ο πρώτος αντιδραστήρας που το κατάφερε αυτό, ήταν ο πειραματικός αντιδραστήρας Chicago Pile-1 στις 2 Δεκεμβρίου 1942, την ίδια στιγμή που η Ευρώπη ήταν βυθισμένη στη τραγική αλληλοεξόντωση του Β παγκόσμιου πολέμου. Προφανώς η ιστορική συγκυρία οδήγησε την έρευνα και στην κατασκευή μίας διάταξης που θα είχε κρισιμότητα πολύ μεγαλύτερη από 1, την ατομική βόμβα. Εκείνη η μέρα του Δεκέμβρη όμως, ήταν η πρώτη μέρα μιας νέας εποχής για την ανθρωπότητα, της πυρηνικής εποχής. Οι Φυσικοί και οι Μηχανικοί, θα έπρεπε πλέον να μελετήσουν τρόπους ώστε να κατασκευαστούν ασφαλείς διατάξεις που θα μπορούσαν να πετύχουν και να διατηρήσουν την κρισιμότητα τους ακριβώς στη μονάδα, έτσι ώστε να μη σβήνουν αλλά και να μην καταστρέφονται. Η θερμότητα των πυρηνικών αντιδραστήρων που θα κατάφερναν να παραμένουν σε κρίσιμη κατάσταση, θα μπορούσε στη συνέχεια να παράξει ηλεκτρισμό όπως στα εργοστάσια καύσης. Αλλά πόσο εύκολο θα ήταν να παραμένει ένας αντιδραστήρας κρίσιμος για μεγάλα χρονικά διαστήματα; Εικόνα 1-3: Καλλιτεχνική απεικόνιση της στιγμής που το Chicago Pile-1 πέτυχε την πρώτη κρισιμότητα (Πηγή: Gary Sheehan) Αλληλεπίδραση νετρονίων με ύλη Τα νετρόνια είναι σωματίδια χωρίς φορτίο, τα οποία στο εσωτερικό ενός αντιδραστήρα έχουν 3 βασικές αλληλεπιδράσεις. Η πρώτη είναι η σκέδαση του νετρονίου στους πυρήνες των υλικών που συναντά κατά την οποία το νετρόνιο χάνει ενέργεια κι επιβραδύνεται (scattering). Η δεύτερη βασική αλληλεπίδραση είναι η απορρόφηση του νετρονίου από κάποιο μη σχάσιμο άτομο (capture). Η τρίτη και βασικότερη είναι η απορρόφηση του νετρονίου από άτομο 235U η οποία οδηγεί στη σχάση (fission). Η πιθανότητα αλληλεπίδρασης σε κάθε διαφορετική περίπτωση, εξαρτάται από ένα μέγεθος που ονομάζουμε μικροσκοπική διατομή του πυρήνα του κάθε στοιχείου, η οποία δεν είναι σταθερή αλλά εξαρτάται από την κινητική ενέργεια του νετρονίου. Καθώς το νετρόνιο προσεγγίζει τον πυρήνα ενός ατόμου, εξαιτίας κβαντικών φαινομένων, η αλληλεπίδραση συμβαίνει όχι μόνο αν το σωματίδιο προσκρούσει στην απειροελάχιστη επιφάνεια του ίδιου του πυρήνα αλλά αν βρεθεί σε μία περιοχή γύρω του. Η περιοχή αυτή που ονομάζεται μικροσκοπική διατομή σ(Ε) μπορεί να είναι δεκάδες χιλιάδες φορές μεγαλύτερη από την πραγματική επιφάνεια του πυρήνα. Σε γενικές γραμμές, για ταχέα νετρόνια με ενέργεια της τάξης των 1-10MeV, όπως δηλαδή συνήθως παράγονται από τη σχάση, οι μικροσκοπικές διατομές απορρόφησης είναι πολύ μικρές και τα νετρόνια αλληλεπιδρούν κυρίως με σκέδαση στα άτομα υδρογόνου ή γραφίτη. Το νετρόνιο ξεκινά με ενέργεια Ε και μετά τη σκέδαση έχει νέα ενέργεια Ε’ για την οποία ισχύει: όπου Α είναι ο μαζικός αριθμός του πυρήνα με τον οποίο το νετρόνιο συγκρούεται. Για Α=1 (υδρογόνο) η ενέργεια του νετρονίου μπορεί ακόμα και να μηδενιστεί με μία μόνο κρούση. Όταν το νετρόνιο πέσει κάτω από 1eV και γίνει θερμικό νετρόνιο οι μικροσκοπικές διατομές των υλικών του αντιδραστήρα μεγαλώνουν σημαντικά με αποτέλεσμα η πιθανότητα να αλληλεπιδράσει μαζί τους να γίνεται εκατοντάδες φορές μεγαλύτερη (Πίνακας 1-1). Μέσα στον αντιδραστήρα όμως δεν υπάρχει ένα νετρόνιο κι ένα μόνο άτομο με τη μικροσκοπική διατομή του αλλά μία ροή νετρονίων και ένας μεγάλος αριθμός ατόμων Ν ανά μονάδα όγκου. Καθώς τα νετρόνια ταξιδεύουν μέσα στο υλικό, όσο μεγαλύτερη είναι η συγκέντρωση στόχων Ν, τόσο μεγαλύτερη κι η πιθανότητα να βρεθούν μέσα στη μικροσκοπική διατομή κάποιου από αυτούς και να αλληλεπιδράσουν μαζί του. Το γινόμενο της μικροσκοπικής διατομής ενός στοιχείου με τη συγκέντρωση ατόμων αυτού του στοιχείου το ονομάζουμε μακροσκοπική διατομή ενός υλικού και οι μονάδες της είναι 1/cm. Η μακροσκοπική διατομή μας επιτρέπει να υπολογίζουμε την πιθανότητα το νετρόνιο να αλληλεπιδράσει διασχίζοντας ένα δεδομένο μήκος μέσα στο εκάστοτε υλικό. Αν το νετρόνιο ταξιδέψει διάστημα x μέσα σε ένα υλικό με μακροσκοπική διατομή σκέδασης Σs, τότε η πιθανότητα να σκεδαστεί δίνεται από το ολοκλήρωμα (4). H πιθανότητα λοιπόν αλληλεπίδρασης για μικρά x είναι γραμμική συνάρτηση του . Αντίστοιχα συμβαίνει για τη μακροσκοπική διατομή της σχάσης Σf και της απορρόφησης (capture) χωρίς σχάση Σc. Γνωρίζοντας τον ορισμό των μακροσκοπικών διατομών, μπορούμε πλέον να εκφράσουμε την κρισιμότητα ως συνάρτηση αυτών των μεγεθών στη σχέση (6). Η σχέση αυτή προκύπτει από την εξίσωση διάχυσης, ένα μοντέλο υπολογισμού της ροής νετρονίων σε αντιδραστήρα που χρησιμοποιείται ευρέως στην πυρηνική τεχνολογία. Όπου Σα = Σf + Σc η συνολική μακροσκοπική διατομή όλων των αλληλεπιδράσεων νετρονίου με νουκλίδιο που καταλήγουν στην απορρόφηση του ενώ ο όρος D∙Bg2 εκφράζει τη διαρροή νετρονίων από τα τοιχώματα του. Ο συντελεστής διάχυσης D, εκφράζει το μήκος που ταξιδεύει το νετρόνιο μέσα στον αντιδραστήρα μέχρι να γίνει θερμικό και το Βg (geometric buckling) προκύπτει από το μέγεθος και τη γεωμετρία του αντιδραστήρα. Όσο μεγαλύτερος ο αντιδραστήρας τόσο μικρότερο το geometric buckling. Τέλος, το ν είναι ο μέσος αριθμός νετρονίων που παράγονται σε μία σχάση, που για το ουράνιο είναι 2,4. Στην ουσία η σχέση (6) έχει στον αριθμητή την πηγή νετρονίων και στον παρανομαστή τις απώλειες νετρονίων. Αν το κέρδος ισούται με τις απώλειες, τότε η κρισιμότητα είναι 1 και η σχάση ουρανίου συνεχίζεται χωρίς να σβήνει ή να υπερθερμαίνεται ο αντιδραστήρας. Προφανώς, αν ο αντιδραστήρας ξεφύγει από την κρίσιμη κατάσταση και θερμανθεί, απαιτούμε να είναι σχεδιασμένος έτσι ώστε η θέρμανση αυτή να τον καταστήσει υποκρίσιμο για να επανέλθει αυτόματα στην επιθυμητή ισορροπία. k<1 : υποκρίσιμος k=1 : κρίσιμος k>1 : υπερκρίσιμος Πίνακας 1-1: Μικροσκοπικές διατομές στοιχείων ομογενούς αντιδραστήρα για δύο ενεργειακές ομάδες (πηγή: JEFF-3.1.1 library using JANIS software) Βήματα προς την κρισιμότητα Για να γίνει αντιληπτό αυτό το ευαίσθητο ισοζύγιο νετρονίων που απαιτείται για να επιτευχθεί κρισιμότητα (k) ίση με 1, θα πρέπει να αναλύσουμε με ένα παράδειγμα πώς οι βασικές αλληλεπιδράσεις των νετρονίων μέσα σε έναν αντιδραστήρα προσθέτουν ή αφαιρούν νετρόνια από το ισοζύγιο. Έστω λοιπόν ότι αφήνουμε 1000 ταχέα νετρόνια στο εσωτερικό ενός αντιδραστήρα που έχει ουράνιο με τη φυσική αναλογία ισοτόπων του, 0,7% 235U και 99,3% 238U. Το ισότοπο 235 όταν απορροφά ένα νετρόνιο μετατρέπεται σε ουράνιο 236 το οποίο είναι εξαιρετικά ασταθές και οδηγείται πολύ συχνά σε σχάση. Το ισότοπο 238 σκεδάζει το νετρόνιο ή το απορροφά και μετατρέπεται σε 239U το οποίο όμως είναι σταθερό ισότοπο. Και τα δύο ισότοπα πάντως αλληλεπιδρούν πολύ συχνότερα με αργά νετρόνια ενέργειας <1eV. Τα 1000 ταχέα αρχικά νετρόνια, προσομοιώνουν τα νετρόνια που παράγονται μετά από σχάση και οι ενέργειες τους είναι 1-10MeV. Τι θα γίνει λοιπόν αν αφεθούν με τυχαίες διευθύνσεις μέσα στον αντιδραστήρα; Σχεδόν όλα θα σκεδαστούν πάνω στους πυρήνες ουρανίου χωρίς να χάσουν σημαντική ενέργεια (σχέση 1 και 2) καθώς οι πυρήνες είναι πολύ μεγαλύτεροι τους. Μετά από ελάχιστο χρόνο, θα φτάσουν στα όρια του αντιδραστήρα όπου θα διαρρεύσουν προς το περιβάλλον. Κάποια ίσως απορροφηθούν. Εισάγαμε λοιπόν 1000 νετρόνια και πολύ σύντομα χάθηκαν όλα, ως διαρροή, είτε ως απορρόφηση. Ο αντιδραστήρας σβήνει. Αυτό σημαίνει ότι η κρισιμότητα του είναι σχεδόν 0. Πρέπει να αυξηθεί η παραγωγή νέων νετρονίων από τα παλιά κι αυτό γίνεται (κυρίως) μέσω σχάσης αφού κατά τη δημιουργία των θυγατρικών πυρήνων απελευθερώνονται και 2-3 ταχέα νετρόνια στο περιβάλλον. Για να προκληθεί συχνότερα σχάση θα πρέπει με κάποιο τρόπο να μειώσουμε την ενέργεια των νετρονίων ώστε να προλάβουν να αλληλεπιδράσουν με το ισότοπο 235 και να το διασπάσουν πριν διαρρεύσουν στο περιβάλλον. Χρειαζόμαστε έναν ρυθμιστή (moderator), ένα υλικό που να απορροφά σπάνια τα νετρόνια αλλά να τα σκεδάζει πολύ πιο συχνά και με κάθε σκέδαση να τους μειώνει την ενέργεια. Όσο πιο μικρός ο ατομικός αριθμός του ρυθμιστή, τόσο πιο πολύ ενέργεια αφαιρεί από το νετρόνιο σε κάθε σκέδαση. Ιδανικός ρυθμιστής είναι ο γραφίτης (άνθρακας) και το νερό (υδρογόνο). Στην περίπτωση του νερού, ο ίδιος ο ρυθμιστής θα μπορεί και να ψύχει τον αντιδραστήρα που όταν επιτύχει k=1 αναμένουμε να παράγει σημαντικά ποσά θερμότητας. Ας προσθέσουμε λοιπόν νερό και ας βυθίσουμε το καύσιμο μας μέσα σε αυτό. Τα 1000 αρχικά νετρόνια πλέον δεν αλληλεπιδρούν μόνο με το καύσιμο αλλά και με τα άτομα του Η και μάλιστα με κάθε σκέδαση τους, η ενέργεια τους μειώνεται μεσοσταθμικά στο μισό! Χρειάζονται περίπου 25 σκεδάσεις ώστε από ταχέα να γίνουν θερμικά δηλαδή αργά όπως τα μόρια ενός αερίου στην ίδια θερμοκρασία. Όταν γίνουν θερμικά θα πρέπει να συναντήσουν κάποιον πυρήνα 235 ώστε να προκαλέσουν σχάση. Όμως η αναλογία του ισότοπου αυτού είναι πολύ μικρή στη φύση, μόλις 0,7%, άρα πιο πιθανό είναι να απορροφηθούν από το ισότοπο 238 ή να διαρρεύσουν. Η κρισιμότητα μας δεν είναι μηδενική αλλά είναι ακόμα, μικρότερη του 1. Τα 1000 νετρόνια δίνουν λίγες σχάσεις, η επόμενη γενιά νετρονίων δεν αριθμεί 1000 αλλά λιγότερα. Μετά από λίγα εκατοστά του δευτερολέπτου ο αντιδραστήρας πάλι σβήνει. Εδώ θα πρέπει να σκεφτούμε τι είναι προτιμότερο για να αυξήσουμε την κρισιμότητα. Να βάλουμε καύσιμο αρκετά πιο εμπλουτισμένο σε 235U σε ποσοστό περίπου 4%, με τη διαδικασία του εμπλουτισμού να είναι εξαιρετικά δαπανηρή και δύσκολη ή να προσθέσουμε ελαφρά πιο εμπλουτισμένο καύσιμο (1,8%) ανάμεσα σε μεγάλες ποσότητες γραφίτη ώστε να αυξήσουμε τη ρύθμιση και να μειώσουμε τη διαρροή νετρονίων; Ο δεύτερος τύπος αντιδραστήρα με γραφίτη είναι πολύ πιο μεγάλος σε μέγεθος αφού θα πρέπει να τοποθετήσουμε σωλήνες καυσίμου και νερού μέσα σε μεγάλα μπλοκ γραφίτη αλλά χρειάζεται λιγότερο εμπλουτισμένο καύσιμο, είναι πολύ πιο φθηνός και φαίνεται προτιμότερος. Η λύση που εφάρμοσε ο Φέρμι στον πειραματικό του αντιδραστήρα Chicago Pile-1 αλλά και οι Σοβιετικοί επιστήμονες σε όλα τα πυρηνικά εργοστάσια τους τη δεκαετία του ’60 ήταν ρύθμιση με γραφίτη. Και πράγματι αυτή η διάταξη λειτούργησε. Ο γραφίτης συγκρατεί τα νετρόνια εντός του αντιδραστήρα και μετά από χιλιάδες σκεδάσεις, αυτά μετατρέπονται σε θερμικά και συναντούν κάποιον πυρήνα 235 ώστε να προκαλέσουν σχάση. Υπάρχει όμως μία σημαντική διαφορά μεταξύ ενός αντιδραστήρα που ρυθμίζεται με νερό κι ενός που ρυθμίζεται με γραφίτη. Ο πρώτος αποδεικνύεται ότι μπορεί να λειτουργεί με μία συνθήκη που ονομάζεται αρνητικός συντελεστής κενού (negative void coefficient) ενώ ο δεύτερος με γραφίτη, έχει θετικό συντελεστή κενού (positive void coefficient). Ο θετικός συντελεστής κενού κάτω από εξαιρετικά σπάνιες συνθήκες, μπορεί να επιταχύνει ένα πυρηνικό ατύχημα. Η πρώτη και τελευταία φορά που διαπιστώθηκε η προβληματική λειτουργία ενός αντιδραστήρα με positive void coefficient, ήταν στο Τσερνόμπιλ. Αναφορές
(1) Dudestadt J., 1976. Nuclear Reactor Analysis (2) Faw R., et al., 2003. Encyclopedia of Physical Science and Technology (Third Edition) (3) Bickel J., 2002. Fundamentals of Nuclear Engineering. Module 5, 9. https://www.nrc.gov/docs/ML1214/ML12142A083.pdf (4) Murray R., 2015. Nuclear Energy. An Introduction to the Concepts, Systems, and Applications of Nuclear Processes Seventh Edition. (5) U.S.N.R.C. Reactor Core & Vessel Design, AP1000 Technology, Chapter 2.0. https://www.nrc.gov/docs/ML1122/ML11221A080.pdf (6) U.S.N.R.C. AP1000 Design Control Document, Chapter 4. Comments are closed.
|


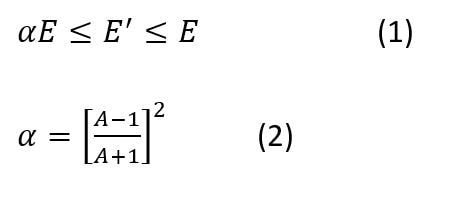
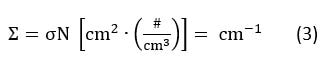
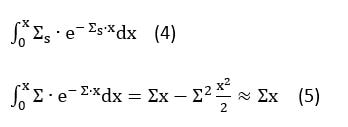
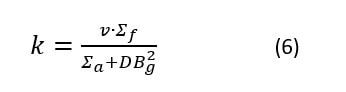
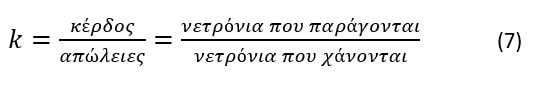
 RSS Feed
RSS Feed