|
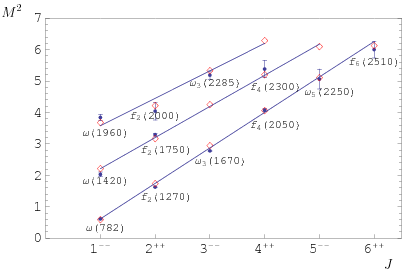
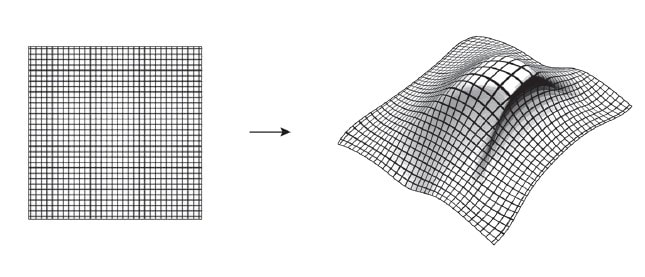
Του Κώστα Φίλιππα Εικόνα 1. Μία καλλιτεχνική απεικόνιση των υπερχορδών (Έργο του RiverFox1). Τα τελευταία εκατό και πλέον χρόνια παραμονής μας στον πλανήτη ετούτο, η επιστημονική κοινότητα έχει αδιαμφισβήτητα πραγματοποιήσει εντυπωσιακά άλματα στο πεδίο της θεωρητικής Φυσικής. Μέσα από την παρατήρηση ότι το φως έχει την ίδια ακριβώς ταχύτητα σε όλα τα συστήματα αναφοράς κι ότι οι νόμοι του Ηλεκτρομαγνητισμού μένουν αναλλοίωτοι υπό τους μετασχηματισμούς του Lorentz (και όχι του Γαλιλαίου), ο απόλυτος χρόνος και χώρος του Νεύτωνα εγκαταλείφθηκαν για τον χωρόχρονο της Ειδικής Θεωρίας της Σχετικότητας [1]. Η δομική αδυναμία της Ειδικής Σχετικότητας να συμπεριλάβει την επιταχυνόμενη παρατηρήτρια και τη βαρύτητα οδήγησαν σχετικά γρήγορα στη Γενική Θεωρία της Σχετικότητας [2], μια ολοκληρωμένη κλασσική (κι όχι κβαντική) θεωρία για τη βαρύτητα. Έπειτα, η ίδια η αδυναμία της κλασσικής Φυσικής να εξηγήσει τη μικροσκοπική δομή της ύλης ώστε να αντιμετωπίσει το πρόβλημα της ακτινοβολίας μέλανος σώματος του Planck και το φωτοηλεκτρικό φαινόμενο του Einstein θεμελίωσαν την Κβαντική Μηχανική [3], μια θεωρία για το μικροσκοπικό, που λίγο πολύ κρατεί ως έχει έναν ολόκληρο αιώνα μετά. Με τη βαρύτητα παραγκωνισμένη στο περιθώριο του μικρόκοσμου, η αμοιβαία έλξη ανάμεσα στην Κβαντομηχανική και την Ειδική Σχετικότητα δεν άργησε να εξελιχθεί σε έρωτα φλογερό, την επονομαζόμενη Κβαντική Θεωρία Πεδίου [4]. Ένα κβαντικό πεδίο γεμίζει όλο τον φυσικό χώρο και η διέγερσή του σε μια συγκεκριμένη περιοχή αποτελεί την οντότητα που συνειδητοποιούμε σήμερα ως σωματίδιο. Για του λόγου το ακριβές, μιας και οι εξισώσεις της θεωρίας δεν νοούν τον χωρόχρονο δίχως τα πεδία αυτά, συνειδητοποιούμε ότι τα κβαντικά πεδία είναι ο ίδιος ο φυσικός χώρος. Η Κβαντική Θεωρία Πεδίου είναι σήμερα η πιο επιτυχημένη φυσική θεωρία, πραγματοποιώντας προβλέψεις για τον τρόπο που αλληλεπιδρούν τα σωματίδια στους επιταχυντές ανά τον πλανήτη με ακρίβεια έως και στα δεκαέξι δεκαδικά ψηφία. Πέραν του ότι η θεωρία των κβαντικών πεδίων αδυνατεί να εγκολπώσει τη βαρύτητα στο μικρόκοσμο, αξίζει να σημειώσουμε ότι τόσο η Κβαντική Μηχανική όσο και η Κβαντική Θεωρία Πεδίου αποτελούν μαθηματικά πλαίσια της Φυσικής και όχι πραγματικά θεμελιώδεις θεωρίες. Τουτέστιν, διεξάγοντας το πείραμα της διπλής σχισμής θεωρούμε ότι ένα (σημειακό) σωματίδιο, ό,τι κι αν είναι αυτό, πρέπει να συμπεριφέρεται ως κύμα πριν από την παρατήρηση του και, οπότε, προτείνουμε ότι βρίσκεται σε μια κατάσταση που περιγράφεται από την κυματοσυνάρτηση , η οποία με τη σειρά της ικανοποιεί την εξίσωση Schrödinger: όπου h η γενικευμένη σταθερά του Planck και η ενέργεια του σωματιδίου. Το τετράγωνο της κυματοσυνάρτησης αυτής μας δίνει την πιθανότητα να εντοπίζεται ένα σωματίδιο εδώ ή εκεί στο χώρο, μια χρονική στιγμή t. Η ουσία εδώ είναι ότι η κυματοσυνάρτηση αναφέρεται στις δυνατές καταστάσεις της ύλης και όχι στην οντολογία της. Το ίδιο ισχύει και για την Κβαντική Θεωρία Πεδίου, η οποία δεν είναι τίποτε άλλο παρά η Κβαντική Μηχανική με άπειρους αρμονικούς ταλαντωτές που αναπαριστούν τις διάφορες διεγέρσεις ενός κβαντικού πεδίου. Οι θεωρίες αυτές, εν ολίγοις, εκκινούν από ορισμένες παραδοχές ή παρατηρήσεις της ανθρώπινης εμπειρίας πάνω στο πως συμπεριφέρονται τα σωματίδια, ενώ δεν εξετάζουν τι εστί ύλη. Ως προς το τι εστί κάτι σημειολογικά, εδώ, να αναφέρουμε ότι κάτι είναι αυτό που είναι επειδή κάνει αυτό που κάνει και δεν κάνει αυτό που κάνει επειδή είναι αυτό που είναι. Στη Φυσική, δηλαδή, όπως και στη φιλοσοφία ή τη γλωσσολογία – κι όπως και σε οποιοδήποτε πεδίο της ανθρώπινης νόησης, εδώ που τα λέμε – η εννοιολόγηση προκύπτει από την αφαίρεση του αντικειμένου από το όλον και την αντιπαραβολή του ως προς αυτό. Από την άποψη αυτή, εάν εξαιρέσουμε τη βαρύτητα, η Κβαντική Θεωρία Πεδίου που περιγράφει τι κάνει η ύλη αρκεί για τη θεμελιώδη περιγραφή του φυσικού κόσμου, κάτι όμως που όπως θα δείξουμε αμέσως δεν μπορεί να ισχύει. Η υπόνοια ότι υποβόσκει μια πιο θεμελιώδης θεωρία της ύλης προκύπτει μέσα από την πολύ βασική παραδοχή της Κβαντικής Θεωρίας Πεδίου ότι τα σωματίδια είναι οντότητες μηδενικής διάστασης στο χώρο: ότι δηλαδή είναι (μαθηματικά) σημεία. Το ότι αυτό δείχνει να μην είναι σωστό έρχεται από δυο ξεχωριστές παρατηρήσεις της φυσικής των μεσονίων. Πρώτον, από το ότι τα μεσόνια κατηγοριοποιούνται σε οικογένειες (τροχιές Regge) όπου, για όλες τους, η στροφορμή είναι ανάλογη του τετραγώνου της μάζας τους. Η σχέση αυτή χαρακτηρίζει οντότητες μοναδιαίας διάστασης και όχι μηδενικής, η οποία και θα προέβλεπε γραμμική σχέση ανάμεσα στη μάζα και τη στροφορμή. Με λίγα λόγια, τα σωματίδια δεν μπορούν να νοηθούν ως σημειακά, αλλά αντίθετα οδηγούμαστε να τα συλλάβουμε ως μονοδιάστατα αντικείμενα, τις χορδές. Η συγκινητική αυτή διαπίστωση φαίνεται να επιβεβαιώνεται κι από το γεγονός ότι όταν απομακρύνουμε τα δυο quarks που συνθέτουν ένα μεσόνιο, η δύναμη που τα κρατά παρέα είναι γραμμικώς ανάλογη της μεταξύ τους απόστασης, χαρακτηριστικό πάλι μιας ανοικτής χορδής που τεντώνεται κατά μήκος των άκρων της. Εικόνα 2: Οι τροχιές Regge στο διάγραμμα M2-J των μεσονίων, από τον Francisco R. Villatoro. Συνειδητοποιώντας μια πραγματικότητα όπου η θεμέλιος λίθος της είναι μια χορδή, θεωρούμε ένα τέτοιο αντικείμενο να πλανιέται μέσα σε έναν επίπεδο -διάστατο χωρόχρονο και εξάγουμε την εξίσωση που περιγράφει την κίνηση του: η οποία δεν είναι άλλη από την κυματική εξίσωση στις δυο διαστάσεις, με c την ταχύτητα του φωτός στο κενό. Τα τ,σ μπορούν να εκληφθούν ως ο χρόνος και το μήκος που αισθάνεται η χορδή για τον εαυτό της, ενώ το εδώ αναπαριστά τη θέση της χορδής αυτής μέσα στον χώρο Μ. Επιλύοντας την παραπάνω κυματική εξίσωση παρέα με τις κατάλληλες συνοριακές συνθήκες ανακαλύπτουμε ότι η χορδή, πέραν μιας ορμής p με την οποία μπορεί να διαδίδεται το γεωμετρικό της κέντρο μέσα στον M, εν γένει ταλαντώνεται ως κύμα σε αρμονικές ιδιοσυχνότητες. Στην πραγματικότητα, η κυματική εξίσωση κίνησής της συνοδεύεται από τους περιορισμούς: από τους οποίους ο πρώτος εκφράζει ότι οι ταλαντώσεις της χορδής είναι αποκλειστικά εγκάρσιες (κάθετες ως προς τη διάσταση της χορδής) ενώ ο δεύτερος υπονοεί ότι τα ελεύθερα άκρα μιας ανοικτής χορδής κινούνται με την ταχύτητα του φωτός. Συνοπτικά, μια χορδή, ανάλογα με την ενέργειά της, δονείται σε συγκεκριμένες αρμονικές συχνότητες. Όσο μεγαλύτερη η ενέργεια της, τόσο μεγαλύτερη και η συχνότητα ταλάντωσης της, και τούμπαλιν. Η ενέργεια όμως είναι η άλλη όψη της μάζας στο νόμισμα της ύλης, οπότε και διαπιστώνουμε ότι: μια χορδή δονούμενη σε συγκεκριμένη συχνότητα αντιπροσωπεύει αυτό που συνειδητοποιούμε σήμερα ως σωματίδιο μιας ορισμένης μάζας. Μια χορδή μπορεί να είναι ανοικτή ή και κλειστή (τοπολογία κύκλου). Ανάγοντας τη χορδή στο κβαντικό επίπεδο, αναβαθμίζοντας δηλαδή το πεδίο της θέσης της X σε κβαντικό, βρίσκουμε ότι η βασική – χαμηλότερη ενεργειακά – κατάσταση και των δυο ειδών χορδής αντιστοιχεί σε αρνητική (τετραγωνική) μάζα και είναι άρα ταχυονική. Το γεγονός αυτό είναι προβληματικό για κάθε σωματιδιακή θεωρία, μιας και ένα ταχυόνιο αντιστοιχεί πάντα σε μια ασταθή κατάσταση. Εικόνα 3: Αναπαράσταση ανοικτών (αριστερά) και κλειστών (δεξιά) χορδών. (Πηγή [5]) Παρακάτω θα δούμε ότι, στην πραγματικότητα, η ταχυονική αυτή κατάσταση εξαιρείται από τη θεωρία με τρόπο φυσιολογικό και συνάμα συναρπαστικό. Αδιαφορώντας για την αγωνία μας έναντι της ταχυονικής συμπεριφοράς της χορδής, εξετάζουμε τον αμέσως επόμενο ενεργειακά δυνατό τρόπο ταλάντωσής της και ανακαλύπτουμε ότι, για την ανοικτή χορδή, αυτή είναι μια άμαζη μποζονική κατάσταση: ενώ για την κλειστή χορδή είναι οι τρεις άμαζες καταστάσεις: όπου το /0;p> αναπαριστά τη βασική κατάσταση της χορδής με ορμή κέντρου μάζας p. Τα κβαντικά πεδία A, h,... δρουν πάνω στη βασική κατάσταση της χορδής ώστε τα αντικείμενα (A/0;p>) κτλ να αναπαραστήσουν την αμέσως επόμενη διεγερμένη κατάστασή της. To Α στην μ δεν είναι άλλο από το γνωστό μας ηλεκτρομαγνητικό πεδίο, ενώ το h με δείκτες μν ταυτίζεται με το πεδίο του βαρυτονίου. Το ηλεκτρομαγνητικό (φωτονικό) πεδίο είναι αυτό που διεγείρεται σε ένα φωτόνιο, το σωματίδιο-φορέα της ηλεκτρομαγνητικής δύναμης, ενώ το βαρυτονικό πεδίο παράγει το βαρυτόνιο, τον υποθετικό φορέα της βαρύτητας. Παρατηρούμε λοιπόν με έκπληξη ότι, εκτός του αγνού ηλεκτρομαγνητισμού, η θεωρία χορδών εμπεριέχει τη βαρύτητα με τρόπο φυσιολογικό, υπό τον όρο βέβαια ότι το πεδίο hμν θα ικανοποιεί τις σωστές εξισώσεις κίνησης: τις εξισώσεις του Einstein. Πράγματι, όπως θα δούμε παρακάτω, αυτό ακριβώς είναι που συμβαίνει. Πριν εξάγουμε την οποιαδήποτε εξίσωση για τη βαρύτητα στη θεωρία των χορδών, θα πρέπει να σμίξουμε την κβαντική χορδή με ένα βαρυτικό πεδίο. Τουτέστιν, αυτή τη φορά, επιθυμούμε να θεωρήσουμε τη χορδή μέσα σε έναν καμπύλο χωρόχρονο, έναντι του επίπεδου χώρου που θεωρούσαμε έως τώρα. Αυτό και πράττουμε, υποθέτοντας μια χορδή σε έναν D-διάστατο κι εν γένει καμπύλο χωρόχρονο M ο οποίος περιγράφεται από το βαρυτικό πεδίο gμν (g με δείκτες μν). Το gμν ονομάζεται μετρικός τανυστής του M και, μέσα σε άλλα, αποδίδει το πόσο καμπυλωμένος είναι ο γεωμετρικός αυτός χώρος. Αμέσως, όμως, γεννιέται και η εξής εύλογη διαπίστωση: εφ' όσον θεωρούμε ότι η χορδή πλανιέται μέσα σε ένα κλασσικό βαρυτικό πεδίο g, ενώ συνάμα το h είναι ο βαρυτονικός τρόπος ταλάντωσης της κλειστής κβαντικής χορδής, το βαρυτικό αυτό πεδίο θα πρέπει κατά έναν κάποιο τρόπο να συντίθεται από τα κβάντα h. Το πρόβλημα λοιπόν διαβάζεται ως το: πώς το (κβαντικό) βαρυτονικό πεδίο h ανάγεται σε (κλασσικό) βαρυτικό g. Το τοπίο καθαρίζει μελετώντας την κβαντική φύση της αλληλεπίδρασης του βαρυτικού πεδίου g με τη χορδή, ανακαλύπτοντας ότι αυτό ισοδυναμεί με μια υπέρθεση (superposition) κβαντικών μικρο-καταστάσεων h. Με τον όρο υπέρθεση στη Κβαντική Μηχανική εννοούμε ότι η συνολική κατάσταση (εδώ του πεδίου g) είναι το άθροισμα πολλαπλών κβαντικών υπό-καταστάσεων, κάθε μια εκ των οποίων έχει τη δική της πιθανότητα να αναδειχθεί ως η μια και μοναδική. Κάθε τέτοια υπό-κατάσταση είναι μια λύση της εξίσωσης Schrödinger που δώσαμε στην αρχή, ενώ το γεγονός ότι όλες οι λύσεις αυτές μπορούν να αθροιστούν σε μια συνολική λύση είναι αποτέλεσμα της γραμμικότητας της εξίσωσης αυτής. Επιστρέφοντας στο επίδικο, το πεδίο βρίσκεται, πιο συγκεκριμένα, σε μια συνεκτική κατάσταση (coherent state) βαρυτονίων, η οποία λίγο-πολύ είναι μια υπέρθεση άπειρων τέτοιων υπο-καταστάσεων του . Δεδομένου ότι το πεδίο είναι κλασσικό, το συμπέρασμα αυτό είναι ακριβοπόθητο μιας και γνωρίζουμε ότι – μαθηματικώς – μια συνεκτική κβαντική κατάσταση είναι ό,τι πιο κοντινό διαθέτουμε στην κλασσική συμπεριφορά. Στη θεωρία χορδών, λοιπόν, με τρόπο φυσιολογικό, ένα κλασσικό βαρυτικό πεδίο κυριολεκτικά συντίθεται από κβαντικές βαρυτονικές χορδές! Εικόνα 4: Ένας μετασχηματισμός Weyl μιας δισδιάστατης επιφάνειας, όπως αυτός συνειδητοποιείται μέσα από τις τρεις χωρικές διαστάσεις. (Εικόνα του συγγραφέα) Όπως ένα σημειακό σωματίδιο σχηματίζει μια κοσμική γραμμή καθώς πλανιέται στον χωρόχρονο, έτσι και μια μονοδιάστατη χορδή σχηματίζει ένα δισδιάστατο κοσμικό φύλλο. Οι επιφάνειες δυο διαστάσεων είναι εκ φύσεως γεωμετρικά ιδιαίτερες, καθώς κατέχουν πάντα μια συμμετρία (1) που δεν εντοπίζουμε σε χώρους διαφορετικής διάστασης: τη συμμετρία Weyl. Περιγραφικά, ένας γεωμετρικός μετασχηματισμός Weyl αλλάζει το σχήμα μιας επιφάνειας, διατηρώντας πάντα τις γωνίες που ορίζονται μεταξύ των παραλλήλων ευθειών της επιφάνειας αυτής. Στις επιφάνειες δυο διαστάσεων όμως, όπως το κοσμικό φύλλο μιας ταξιδιάρας χορδής, ο μετασχηματισμός αυτός δεν αλλάζει τίποτε και ως εκ τούτου λέμε ότι αποτελεί μια συμμετρία του (2). [1] Συμμετρία είναι ένας μετασχηματισμός που δρα σε ένα αντικείμενο, ή και σε μια θεωρία, και το αφήνει αναλλοίωτο. [2] Εδώ μπορεί να αισθανθούμε ότι η πρόταση αυτή είναι λάθος, καθώς μπορούμε εύκολα να οπτικοποιήσουμε μια αλλοίωση Weyl σε μια δισδιάστατη επιφάνεια. Παρ’ όλα αυτά, η οπτικοποίηση αυτή είναι ο τρόπος που αντιλαμβανόμαστε μια τέτοια επιφάνεια στις τρεις δικές μας χωρικές διαστάσεις. Ένα δισδιάστατο υποθετικό ον δεν θα αισθανόταν οποιαδήποτε παρενόχληση από τον κύριο Weyl. Η συμμετρία Weyl του κοσμικού φύλλου, παρ' όλα αυτά, ισχύει ανέξοδα μονάχα στο κλασσικό επίπεδο. Εάν δεν απαιτήσουμε την κβαντική θεωρία ως Weyl-συμμετρική, τότε η συμμετρία αυτή σπάει στο κβαντικό επίπεδο, είναι δηλαδή ανώμαλη στο λεξιλόγιο της Κβαντικής Θεωρίας Πεδίου. Στην περίπτωση αυτή, οι θεωρίες χορδών που παράγονται είναι εν γένει μαθηματικά ασυνεπείς και ονομάζονται μη-κρίσιμες. Στο κβαντικό επίπεδο, μελετώντας τις κβαντικές διορθώσεις της θεωρίας σε πρώτη τάξη, ώστε η χορδή να διατηρεί αυτή την συμμετρία θα πρέπει να ισχύει: όπου Rμν είναι ο λεγόμενος τανυστής καμπυλότητας του Ricci για τον καμπύλο χωρόχρονο M, ενώ η σχέση αυτή κατανοείται ως οι εξισώσεις κίνησης του βαρυτικού υποβάθρου μέσα στο οποίο ζει η χορδή. Το αποτέλεσμα αυτό ξεπερνά κάθε μας προσδοκία, μιας και οι παραπάνω εξισώσεις δεν είναι άλλες από τις εξισώσεις του Einstein στον κενό χώρο! Με άλλα λόγια, όπως ακριβώς υποσχεθήκαμε να δείξουμε, η Γενική Σχετικότητα εμπεριέχεται φυσιολογικά στη θεωρία των χορδών. Εικόνα 5: Αναπαράσταση χορδών από τον Victor de Schwanberg Σαν να μην αρκούσε η ανάδυση των κλασσικών εξισώσεων της βαρύτητας, μελετώντας τις κβαντικές διορθώσεις δευτέρας τάξης της χορδής, αποκτάμε την θεωρητική διόρθωση των εξισώσεων του Einstein: όπου Rμκρσ ο λεγόμενος τανυστής καμπυλότητας του Riemann και α΄ μια κλίμακα μεγέθους του μήκους της κβαντικής χορδής. Πιθανότατα, αμέσως αισθανόμαστε μια έντονη προσδοκία να ελέγξουμε τη διόρθωση αυτή της κλασσικής βαρύτητας, ώστε να αποκτήσουμε την πρώτη πειραματική εγκυρότητα για τη θεωρία αυτή κβαντικής βαρύτητας. Εξάλλου, οι ίδιες δοκιμασίες που ανέδειξαν την ισχύ της Γενικής Σχετικότητας – η μετάπτωση του περιηλίου του Ερμή, η καμπύλωση του φωτός από τον Ήλιο μας και η βαρυτική ερυθρά μετατόπιση του φάσματος του φωτός – είναι πάντα στη διάθεση οποιασδήποτε θεωρίας επιθυμεί να αντιπροτείνει μια πρόβλεψη στα μετρούμενα νούμερα. Δυστυχώς, όμως, ως προς το ζήτημα της ανθρώπινης υπομονής, η παραπάνω θεωρητική διόρθωση αποδεικνύεται υπερβολικά μικρή για να ανιχνευθεί. Προς το παρόν, δηλαδή. Η θεωρία των χορδών που αναπτύξαμε έως τώρα, παρ' όλη την ομορφιά της, πάσχει από δυο βασικά μειονεκτήματα. Για αρχή, αναφέρεται μονάχα στη μποζονική χορδή, το είδος δηλαδή της γεωμετρικής χορδής που αντιστοιχεί σε μποζονικά πεδία και όχι σε φερμιονικές καταστάσεις της ύλης. Έπειτα, όπως ήδη αναφέραμε, η βασική της (μποζονική) κατάσταση είναι ταχυονική και άρα ασταθής. Η σωστή εξέλιξη της θεωρίας έρχεται κατά τα αναμενόμενα, εμπεριέχοντας τη φερμιονική πλευρά της χορδής. Μελετώντας την ενισχυμένη θεωρία, ανακαλύπτουμε ότι για να έχει φυσικό νόημα ο φερμιονικός τομέας της χορδής θα πρέπει να συμπεριλάβουμε ένα νέο είδος συμμετρίας, την επονομαζόμενη υπερσυμμετρία (supersymmetry). Η υπερσυμμετρία είναι το μοναδικό αυτό είδος συμμετρίας που ορίζει οτι κάθε μποζόνιο έχει έναν (υπερσυμμετρικό) φερμιονικό έταιρο και τούμπαλιν, η οποία – ενώ ανακαλύφθηκε ως φάρμακο για την πάσχουσα φερμιονική χορδή – ανήχθη σε ένα από τα κυρίαρχα πεδία έρευνας στην ευρύτερη θεωρητική Φυσική των στοιχειωδών σωματιδίων. Στο επίπεδο της κβαντικής χορδής, η υπερσυμμετρία πολύ απλά ορίζει ότι κάθε μποζονικός τρόπος ταλάντωσής της αντιστοιχεί σε έναν φερμιονικό ίδιας ενέργειας. Τελικά, η εκ νέου μελέτη της υπερσυμμετρικής χορδής αποκαλύπτει ότι η ταχυονική βασική κατάσταση παύει να υφίσταται. Έτσι, οι άμαζες μποζονικές καταστάσεις που βρήκαμε αρχικά (παρέα με αντίστοιχες τώρα φερμιονικές) παίρνουν τα σκήπτρα ως οι νέες βασικές καταστάσεις της (ανοικτής ή κλειστής) χορδής, σταθεροποιώντας άρα ξαφνικά τη θεωρία! Μάλιστα, προκειμένου να είναι το συνολικό οικοδόμημα μαθηματικά συνεπές προκύπτει ότι η διάσταση του χωροχρόνου M, μέσα στον οποίο κινείται η υπερχορδή, θα πρέπει να έχει διάσταση D=10. Η θεωρία των υπερχορδών, όπως την ονομάζουμε, έχει τόσο εκθαμβωτικό περιεχόμενο που θα μπορούσαμε να φλυαρούμε σε αμέτρητες σελίδες για τους ορίζοντες που έχει ανοίξει στο πεδίο της μαθηματικής Φυσικής. Για λόγους ουσίας, παρ' όλα αυτά, θα προτιμήσουμε μια αριστοτεχνική κωλοτούμπα ώστε να επιστρέψουμε στη βάση και να κατανοήσουμε τη σημερινή επιστημονική θεωρία ως ιστορική διαδικασία και όχι ως κάτι απόλυτο ή εξωτερικό από τις πρακτικές μας. Eικόνα 6: Υπερσυμμετρικά σωματίδια από B.Gilliland. Ως ιστορική διαδικασία, η επιστήμη έχει οικοδομηθεί πάνω στα προνόμια του κόσμου αυτού, ενώ είναι πάντα μια αντανάκλαση ολόκληρου του πολιτικού και ιδεολογικού περιεχομένου της κοινωνίας των ανθρώπων. Τι εννοούμε όμως εδώ; Αρχικά, ότι παραδοσιακά την επιστήμη την έχουν ασκήσει αυτοί/ες που είχαν το προνόμιο της πρόσβασης στο πανεπιστήμιο. Έως και σχετικά πρόσφατα, το προνόμιο της πρόσβασης στον ακαδημαϊσμό ταυτιζόταν με το κοινωνικό προνόμιο στη βάση του φύλου, της φυλής και της τάξης. Έτσι, μέχρι και πριν ελάχιστες δεκαετίες, το να ήσουν γυναίκα, μαύρος/η ή φτωχός/ή (ή πολλές φορές και τα τρία μαζί) είχε να πει ότι πολύ απλά δεν είχες πρόσβαση στο να ασκήσεις μια επιστήμη. Με άλλα λόγια, για δεκαετίες ατελείωτες, από όλα τα διαθέσιμα μυαλά μόνον οι προνομιούχοι είχαν την ευκαιρία να ξεδιπλώσουν το ταλέντο τους. Και η αλήθεια είναι πως οι προνομιούχοι κουβαλάνε μέσα στην επιστημονική τους σκέψη και την κουλτούρα των προνομιούχων. Όπως ο αστός και θρησκόληπτος Νεύτωνας, που με υλικό κίνητρο τις τεχνολογικές ανάγκες της πολεμικής βιομηχανίας της εποχής κατά την ανάδυση του εμπορικού κεφαλαίου, ίδρυσε την κλασσική μηχανική μέσα σε έναν απόλυτο χώρο και χρόνο. Όπως η κβαντομηχανική μη-αιτιότητα των Heisenberg, Jordan και Born που ήρθε ως μια ιδεαλιστική αναπαράσταση της κουλτούρας της Βαϊμάρης, όπου η αιτιοκρατία θεωρείτο παιδί του Διαφωτισμού τον οποίον και μισούσαν ορκισμένα. Οι εξισώσεις της Κβαντικής Μηχανικής, από την οποία λίγο πολύ εκκινούμε πάντα, επιδέχονται περισσότερες της μιας ερμηνείες ως προς το τι αναπαριστούν εξ' αυτού που συνειδητοποιούμε ως πραγματικότητα. Κι όμως, είναι η ερμηνεία της Κοπεγχάγης που έχει επικρατήσει εδώ κι έναν αιώνα, δίχως να δόθηκε ποτέ ιδιαίτερη προσοχή στις ανταγωνιζόμενες θεωρήσεις. Έχει σημασία να κατανοήσουμε τι σημαίνει όλο αυτό. Ο/η σύγχρονος/η επιστήμονας έχει την τάση να αντιλαμβάνεται ένα τέτοιο γεγονός ως την ποιοτική υπερίσχυση της τωρινής κυρίαρχης θεωρίας. Αυτό όμως είναι μια αντίληψη υπερβατική: πολλές φορές, το γεγονός ότι μια θεωρία είναι κυρίαρχη είναι αυτό ακριβώς που της έχει δώσει μεταγενέστερα αξία στο ακαδημαϊκό χρηματιστήριο, λησμονώντας τον τρόπο με τον οποίο η ίδια έφτασε αρχικά να κυριαρχήσει. Φυσικά, δεν εννοούμε εδώ ότι η κβαντομηχανική ερμηνεία της Κοπεγχάγης είναι για τα μπάζα, κάθε άλλο, απλώς εξηγούμε την φύση της αξίας που απέκτησε έναντι των ανταγωνιστών της. Πως θα είχαν εξελιχθεί τα πράγματα εάν είχε επενδυθεί εξίσου ερευνητική ενέργεια και χρήμα στην κβαντομηχανική ερμηνεία του Bohm – μέσα από τις λεγόμενες κρυμμένες μεταβλητές – η οποία απορρίφθηκε ως προβολή στο πρόσωπο ενός νεαρού κομμουνιστή τον οποίον και εξόρισαν κυριολεκτικά στη Βραζιλία δίχως χρηματοδότηση και διασυνδέσεις; Μπορεί το ίδιο, μπορεί και όχι [9, 10]. Ο πραγματικός στόχος εδώ δεν είναι να σχηματίσουμε μια κριτική πάνω στο πώς η καπιταλιστική κοινωνία παράγει την επιστήμη της, αν και κάτι τέτοιο θα ήταν σίγουρα εξαιρετικά παραγωγικό. Αντίθετα, η ουσία είναι να κατανοήσουμε τη φύση της σημερινής δομής της επιστημονικής σκέψης ως αυτό που πραγματικά είναι: το μακροχρόνιο αποτέλεσμα του κοινωνικού ανταγωνισμού σε όλες του τις μορφές και εκφράσεις. Αλλιώς: σε ένα όχι και τόσο μακρινό σύμπαν όπου το εμπόρευμα και η κοινωνική τάξη θα ήταν ανέκδοτα για τις ώρες της ατελείωτης τεμπελιάς μας κι όπου η διεμφυλική ταυτότητα δεν θα υπήρχε ως σημείο καταπίεσης κι αγώνα αλλά ως πραγματική συνθήκη, ε λοιπόν σε αυτό το σύμπαν η Φυσική θα ήταν κάτι το εντελώς διαφορετικό. Στα πλαίσια της θεωρητικής Φυσικής, μόνον όταν κατανοήσουμε το βάθος των κοινωνικών μας σχέσεων θα είμαστε σε θέση να αποδομήσουμε τη σύγχρονη επιστημονική μορφή, ώστε να μπορέσουμε να υπερβούμε τα όρια μας και να επαναπροσδιορίσουμε αυτό που έχει προκύψει να συνειδητοποιούμε σήμερα ως πραγματικότητα. Αναφορές
Comments are closed.
|

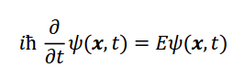
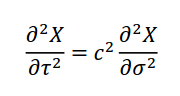
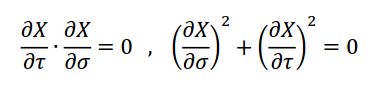
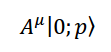
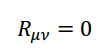

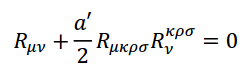
 RSS Feed
RSS Feed