|
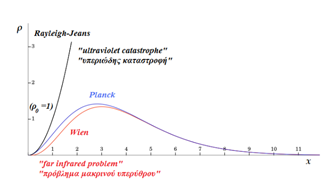
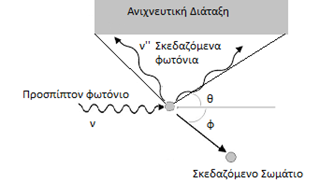
Του Γιώργου Μελαχροινού Στο πρώτο μέρος του άρθρου με τίτλο “Προς τη θεωρία του Καθιερωμένου Προτύπου” παρουσιάστηκαν οι σταδιακές προσπάθειες και έρευνες που έγιναν για την μελέτη και τη κατανόηση της φυσικής του ατόμου. Μέχρι στιγμής μπορούσαμε να περιγράψουμε τα πάντα με απλές κλασικές εξισώσεις ή ακόμα και με απλή γεωμετρία όπως μπορεί να κάνει κανείς στην σκέδαση Rutherford προκειμένου να υπολογίσει τις γωνίες σκέδασης των σωματιδίων α από τους πυρήνες χρυσού. Ωστόσο η θεωρία μας, έτσι όπως την έχουμε φτιάξει μέχρι στιγμής αποτυγχάνει να εξηγήσει την ευστάθεια του ατόμου και προβλέπει ακριβώς αντίθετα αποτελέσματα. Επίσης ένα ακόμη σημείο που η θεωρία μας αποτυγχάνει να εξηγήσει είναι και τα φάσματα εκπομπής των ατόμων, στα οποία ενώ θα αναμέναμε ολόκληρες περιοχές με φως παρατηρούμε μεμονωμένες διακριτές φωτεινές γραμμές. Αντίστοιχα και στα φάσματα απορρόφησης ενώ θα περιμέναμε τα άτομα να απορροφούν ολόκληρες μπάντες-περιοχές από μήκη κύματος, στην πραγματικότητα απορροφούν συγκεκριμένα μόνο μήκη κύματος. Εάν εγκλωβίσουμε αέριο υδρογόνο μέσα σε ένα δοχείο στα άκρα του οποίου έχουμε τοποθετήσει δύο μεταλλικούς ακροδέκτες έτσι ώστε να μπορούμε να εφαρμόσουμε μια διαφορά δυναμικού και να δημιουργήσουμε ένα ηλεκτρικό πεδίο, τότε, αν χρησιμοποιήσουμε μια κατάλληλη διάταξη που λέγεται φασματογράφος, θα δούμε ότι το αέριο εκπέμπει φως συγκεκριμένου χρώματος σε συγκεκριμένες μόνο γωνίες (περισσότερες λεπτομέρειες για την φασματοσκοπία μπορεί να βρει κανένας στην άσκηση 7 του παρακάτω εργαστηριακού οδηγού). Αυτή η εκπομπή του φωτός που αποτυπώνεται στην παραπάνω εικόνα είναι χαρακτηριστική υπογραφή του συγκεκριμένου αερίου. Αντίστοιχα μπορούμε να καταγράψουμε και τα φάσματα απορρόφησης, που είναι τα μήκη κύματος που θα απορροφηθούν όταν φως «πέσει» επάνω στο συγκεκριμένο αέρια. Κάτω: το φάσμα απορρόφησης του Υδρογόνου. Ο λόγος για τον οποίο οι κλασσικές θεωρίες αποτυγχάνουν να εξηγήσουν το φάσμα εκπομπής του υδρογόνου όπως και την σταθερότητά του είναι ότι δεν εμπεριέχουν ανταλλαγές ενέργειας με διακριτό (κβαντισμένο) τρόπο. Η κβαντική μηχανική είναι άρρηκτα συνδεδεμένη με την περιγραφή του μικρόκοσμου. Η ανάγκη για την γένεσή της μας πηγαίνει πίσω στο 1860 όπου διατυπώθηκε το πρόβλημα της ακτινοβολίας του μέλανος σώματος ή αλλιώς το Black Body Radiation Problem. Το πρόβλημα αυτό της ακτινοβολίας του μέλανος σώματος διατυπώνεται λίγο μετά την βιομηχανική επανάσταση, μία περίοδο στην οποία όλοι οι μεγάλοι επιστήμονες προσπαθούν να κατανοήσουν και να μελετήσουν τη θερμοδυναμική και τις μηχανές. Την περίοδο αυτή, οι φυσικοί μπορούν και περιγράφουν τα πάντα χρησιμοποιώντας κλασική φυσική όπως έχει διατυπωθεί τους δύο προηγούμενες αιώνες. Το μέλαν σώμα (black body) είναι ένα εξιδανικευμένο φυσικό σώμα το οποίο απορροφά όλη την προσπίπτουσα σε αυτό ηλεκτρομαγνητική ακτινοβολία ανεξαρτήτως συχνότητας και ανεξαρτήτως γωνίας πρόσπτωσης. Το μέλαν σώμα αφήνει όλη την προσπίπτουσα ακτινοβολία να μπει μέσα του, δηλαδή ανακλά μηδενικό ποσοστό της προσπίπτουσας ακτινοβολίας, και απορροφά όλη αυτή την προσπίπτουσα ακτινοβολία χωρίς να αφήνει ακτινοβολία να το διαπεράσει. Άρα ένα μέλαν σώμα είναι ένας τέλειος απορροφητής της προσπίπτουσας ΗΜ ακτινοβολίας. Βεβαίως, αν συνέβαιναν μόνο τα παραπάνω, τότε λόγω της συνεχούς απορρόφησης ενέργειας, η θερμοκρασία του σώματος θα αυξανόταν συνεχώς. Έτσι, ένα μέλαν σώμα που βρίσκεται σε θερμοδυναμική ισορροπία, άρα και σε σταθερή θερμοκρασία, θα πρέπει να επανεκπέμπει ηλεκτρομαγνητική ακτινοβολία, την οποία καλούμε ακτινοβολία μέλανος σώματος (black-body radiation), έτσι ώστε να διατηρείται το ενεργειακό ισοζύγιο. Στην πράξη το μέλαν σώμα είναι ένα ιδανικό σώμα το οποίο δεν υπάρχει στην φύση καθώς κανένα υλικό δεν φτάνει σε 100% απορρόφηση. Στην καλύτερη περίπτωση η απορρόφηση φτάνει στο 95%, όπως συμβαίνει για παράδειγμα στο γραφίτη. Εκείνη την εποχή, ως μέλανα σώματα χρησιμοποιούσαν κοιλότητες τα τοιχώματα των οποίων ήταν καλυμμένα από γραφίτη. Οι κοιλότητες διατηρούνταν σε μια σταθερή θερμοκρασία και σε κάποιο σημείο του τοιχώματος άνοιγαν μια μικρή οπή ώστε να μπορεί να μπει ηλεκτρομαγνητική ακτινοβολία στο εσωτερικό της κοιλότητας, να απορροφηθεί μετά από πολλαπλές ανακλάσεις και να μπορέσει στη συνέχεια να επανεκπεμφθεί και να καταγραφεί. Ένα μέλαν σώμα εκπέμπει ηλεκτρομαγνητική ακτινοβολία με τρόπο που ακολουθεί την μπλε κατανομή της παρακάτω εικόνας. Όμως σύμφωνα με την κλασική θεωρία ένα σώμα το οποίο θα βρίσκεται σε κάποια θερμοκρασία θα πρέπει να εκπέμπει ΗΜ ακτινοβολία με τρόπο που θα υπακούει στη μαύρη καμπύλη. Εικόνα 2. Οι νόμοι των Rayleigh-Jeans, Wien και Planck ως συνάρτηση του. Πηγή: Κβαντική Οπτική και Lasers, Κ. Σιμσερίδης (2015). Πρέπει να προσέξουμε ότι στην περιοχή του υπεριώδους, που βρίσκεται σε μικρότερα μήκη κύματος απ ́ αυτά του ορατού του ηλεκτρομαγνητικού φάσματος, η καμπύλη αυτή αποκλίνει οδηγώντας σε αυτό που ονομάζεται υπεριώδης καταστροφή και περιγράφεται από τον νόμο Rayleigh-Jeans. Σύμφωνα με αυτό το νόμο η πυκνότητα της ενέργειας ανά συχνότητα ν δίνεται από τη σχέση: Με μονάδες ρ = J m -3 Hz-1 και kB = 1.38064852 × 10 -23 J K-1 η σταθερά του Boltzmann. Στην πράξη όμως οι μετρήσεις έδειξαν ότι οι κατανομές δεν συμφωνούσαν με τις κλασικές καμπύλες. Στην προσπάθεια να ερμηνευτούν οι παρατηρούμενες καμπύλες διατυπώθηκαν δύο νόμοι, ο νόμος του Wien και ο νόμος των Stefan-Boltzmann. Και οι δύο νόμοι εμφανίστηκαν στην προσπάθεια να περιγραφούν οι πειραματικές καμπύλες με σχέσεις. Ο νόμος του Wien, εμφανίστηκε ως μια προσπάθεια να περιγραφούν τα πειραματικά δεδομένα στα χαμηλά μήκη κύματος - υψηλής συχνότητες. Σύμφωνα με το νόμο του Wien η πυκνότητα της ενέργειας (ανά μονάδα όγκου) ανά συχνότητα περιγράφεται από: όπου h = 6.62607004 × 10−34 J · s η σταθερά του Planck. ́Ίσως η πιο σημαντική απόρροια του νόμου του Wien είναι ότι καταφέρνει να συνδέσει τη θέση μεγίστου της κατανομής με την θερμοκρασία του μέλανος σώματος. Απλή παραγώγιση της παραπάνω σχέσης ως προς τη συχνότητα και μηδενισμός αυτής (ώστε να βρούμε το ακρότατο και αντικατάσταση της συχνότητας με τη σχέση c = λ · ν ώστε να υπολογίσουμε το μήκος κύματος) οδηγεί στη σχέση: όπου το μήκος κύματος είναι εκφρασμένο σε μέτρα m και η θερμοκρασία σε Kelvin Κ. Ο νόμος των Stefan-Boltzmann εκφράζεται με δύο τρόπους. Η πρώτη έκφραση δίνει την πυκνότητα της ΗΜ ακτινοβολίας (προκύπτει με ολοκλήρωση του νόμου Planck πάνω στις συχνότητες. Ωστόσο η δεύτερη έκφραση είναι αυτή που έχει το μεγαλύτερο ενδιαφέρον και συνδέει την συνολική εκπεμπόμενη ισχύ του μέλανος σώματος με την θερμοκρασία του ως εξής [1][2]: Λίγα χρόνια αργότερα, το 1877, διατυπώθηκε από τον Boltzmann η ιδέα ότι οι ενεργειακές καταστάσεις των φυσικών συστημάτων μπορεί να είναι διακριτές. Προκειμένου να εξηγηθεί και να κατανοηθεί το φωτοηλεκτρικό φαινόμενο που ανακαλύφθηκε το 1887 από τον Hertz οδήγησαν στην κατεύθυνση της υπόθεσης για την ύπαρξη κβάντων φωτός. Η πραγματική επανάσταση όμως ήρθε το 1905 όταν ο Einstein υπέθεσε ότι η ενέργεια του φωτονίου δίνεται από τη σχέση E = hν, όπου h η σταθερά που πήρε το όνομα του Planck και ν η συχνότητα της ακτινοβολίας και έτσι κατάφερε να εξηγήσει το φωτοηλεκτρικό φαινόμενο και να πάρει το βραβείο Nobel το 1921. Ο νόμος του Planck (1900) [3] ο οποίος περιγράφει την εκπομπή μέλανος σώματος και συμφωνεί με τα πειραματικά δεδομένα είναι: Τα θεμέλια της κβαντικής μηχανικής έχουν μόλις τεθεί. Μία πολύ χρήσιμη και δυνατή σχέση που εμφανίστηκε (την μαθηματική απόδειξη της οποίας μπορεί να διαβάσετε εδώ) είναι η σχέση αβεβαιότητας του Heisenberg για την θέση και την ορμή ενός σωματιδίου: όπου h bar = h/2π, η ανηγμένη σταθερά του Planck. Μια πολύ απλοϊκή απόδειξη για την παραπάνω σχέση αποτελεί το παρακάτω: Για να μπορέσουμε να βρούμε ένα σωμάτιο στο χώρο πρέπει να μετρήσουμε τη θέση του. Για να μπορέσουμε να μετρήσουμε τη θέση του όμως, πρέπει το συγκεκριμένο σωμάτιο να αλληλεπιδράσει με φωτόνια το οποία θα σκεδαστούν και θα φτάσουν σε κάποια ανιχνευτή διάταξη. Το πρόβλημα είναι ότι στην ανιχνευτική διάταξη δεν φτάνει ένα φωτόνιο το οποίο έχει καθορισμένη ορμή, αλλά φτάνουν φωτόνια ανάμεσα σε ένα εύρος συχνοτήτων οπότε δεν μπορούμε μέσω φαινομένου Compton να προσδιορίσουμε την ορμή του σωματιδίου. Εικόνα 3: Σύμφωνα με το φαινόμενο Compton τα σκεδαζόμενα φωτόνια ανάλογα με την γωνία εκπομπής έχουν και διαφορετική συχνότητα. Σημειώνεται δε πως μόνο τα φωτόνια που βρίσκονται εντός του κώνου που βλέπει την ανιχνευτική διάταξη ανιχνεύονται και χρησιμοποιούνται για την καταγραφή της θέσης του σωματιδίου. Λόγω λοιπόν του ότι φτάνει ένα πλήθος από φωτόνια στην ανιχνευτική διάταξη με διαφορετικές συχνότητες τα οποία έχουν αλληλεπιδράσει με το σωμάτιο επηρεάζοντας την ορμή του δεν μπορούμε να προσδιορίσουμε με ακρίβεια την ορμή του. Σύμφωνα με αυτή τη σχέση (πρέπει να προσέξουμε ότι οι ποσότητες x , p συνοδεύονται από το σύμβολο ˆ. Πρόκειται για το σύμβολο του τελεστή. Στο επόμενο άρθρο θα συζητηθεί αναλυτικότερα η έννοια του τελεστή. Μέχρι τότε μπορείτε να διαβάσετε εδώ) όταν καταφέρουμε να περιορίσουμε ένα σωματίδιο στο χώρο τείνοντας την αβεβαιότητα της θέσης του στο μηδέν (∆→ 0) τότε προκειμένου να ικανοποιείται η συγκεκριμένη ανισότητα πρέπει η αβεβαιότητα της ορμής (∆) να τείνει στο άπειρο ώστε το γινόμενο των δύο αβεβαιοτήτων να τείνει σε κάτι πεπερασμένο και μεγαλύτερο του. Η εξήγηση της ευστάθειας του ατόμου του υδρογόνου έγκειται σε αυτήν ακριβώς την ανισότητα καθώς όταν το ηλεκτρόνιο πλησιάσει τόσο πολύ τον πυρήνα του ατόμου ώστε η αβεβαιότητα στη θέση του να τείνει στο μηδέν, η αβεβαιότητα της ορμή που αποκτά είναι τεράστια και έτσι μπορεί πλέον να αποκτήσει οποιαδήποτε ορμή και να βρεθεί παντού στο χώρο. Έτσι κάναμε ένα πρώτο βήμα για να εξηγήσουμε την ευστάθεια του ατόμου. Στο επόμενο άρθρο θα δούμε πώς μπορεί κανείς να μελετήσει το συγκεκριμένο σύστημα με αυστηρά μαθηματικά χρησιμοποιώντας την εξίσωση του Schrӧdinger και την σχέση μετάθεσης των τελεστών της θέσης και της ορμής. Θα δούμε ότι θα καταφέρουμε να εξηγήσουμε, τουλάχιστον μέχρι κάποια σε τάξη ακριβείας, τα φάσματα εκπομπής στο άτομο του υδρογόνου. Θα προκύψουν όμως δυο προβλήματα. Το πρώτο είναι το αποτέλεσμα του πειράματος των Stern-Gerlach, το οποίο αποκάλυψε μια περίεργη συμπεριφορά των ατόμων μέσα σε μαγνητικά πεδία. Το δεύτερο είναι ότι προκειμένου να είμαστε συμβατοί με την ειδική θεωρία σχετικότητας του Einstein θα πρέπει η δυναμική, δηλαδή το σύνολο των εξισώσεων που περιγράφουν ένα σύστημα να είναι συμβατό να υπακούουν τους μετασχηματισμούς Lorentz. Έτσι θα οδηγηθούμε σε μία εξίσωση, την Klein-Gordon που θα καταφέρει να λύσει το δεύτερο πρόβλημα ωστόσο το πρώτο πρόβλημα θα παραμείνει άλυτο. Αναφορές
Comments are closed.
|


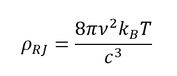
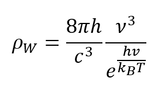
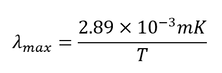
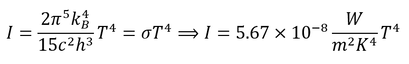
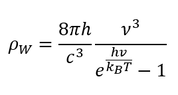
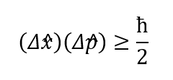
 RSS Feed
RSS Feed